Explanation
KNOBS is the keyword for the data block. Optionally, DEBUG .
Line 1: -iterations iterations
-iterations --Allows changing the maximum number of iterations. Default is 100 at startup. Optionally, iterations or -i [ terations ].
iterations --Positive integer limiting the maximum number of iterations used to solve the set of algebraic equations for a single calculation. Values greater than 200 are not usually effective.
Line 2: -convergence_tolerance convergence_tolerance
-convergence_tolerance
--Changes the convergence criterion used to determine when the algebraic equations have been solved. For an element mole-balance equation, convergence is satisfied when mole balance is within
convergence_tolerance
times the total moles of the element (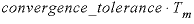
). When the
-high_precision
identifier of SELECTED_OUTPUT is true, the convergence criterion is set to the smaller of
convergence_tolerance
and 1
×
10
-12
. Default is 1
×
10
-8
at startup. Optionally,
convergence_tolerance
or
-c
[
onvergence_tolerance
].
convergence_tolerance --Tolerance for determining convergence in the nonlinear equation solver.
-tolerance --Allows changing the tolerance used by the optimization solver (subroutine cl1) to determine numbers equal to zero. This is not the convergence criterion used to determine when the algebraic equations have been solved. At starutp, default is 1 × 10 -15 (or possibly smaller if the program is compiled with long double precision). Optionally, tolerance or -t [ olerance ].
tolerance --Positive, decimal number used by the optimization solver (subroutine cl1). All numbers smaller than this number are treated as zero. This number should approach the value of the least significant decimal digit that can be interpreted by the computer. The value of tolerance should be on the order of 1 × 10 -12 to 1 × 10 -15 for most computers and most simulations.
-step_size --Allows changing the maximum step size. At startup, default is 100; activities of master species may change by up to 2 orders of magnitude in a single iteration. Optionally, step_size or -s [ tep_size ].
step_size --Positive, decimal number limiting the maximum, multiplicative change in the activity of an aqueous master species on each iteration.
Line 5: -pe_step_size pe_step_size
-pe_step_size --Allows changing the maximum step size for the activity of the electron. Optionally, pe_step_size or -p [ e_step_size ].
pe_step_size
--Positive, decimal number limiting the maximum, multiplicative change in the conventional activity of electrons on each iteration. Normally,
pe_step_size
should be smaller than the
step_size
because redox species are particularly sensitive to changes in pe. Default is 10; that is,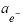 
may change by up to 1 order of magnitude in a single iteration or pe may change by up to 1 unit.
Line 6: -diagonal_scale [( True or False )]
-diagonal_scale --Allows changing the default method for scaling equations. Invoking this alternative method of scaling causes any mole-balance equations with the diagonal element (approximately the total concentration of the element or element valence state in solution) less than 1 × 10 -10 to be scaled by the reciprocal of the diagonal element. Default is false at startup. Optionally, diagonal_scale or -d [ iagonal_scale ].
( True or False )--A value of true indicates the alternative scaling method is to be used; false indicates the alternative scaling method will not be used. If neither true nor false is entered on the line, true is assumed. Optionally, t [ rue ] or f [ alse ].
Line 7: -debug_diffuse_layer [( True or False )]
-debug_diffuse_layer --Includes debugging prints for diffuse layer calculations. This identifier applies only when -diffuse_layer is used in the SURFACE data block. If this option is set to true , values of the g function--the surface excess--are printed for each value of charge for aqueous species; the charge(s) for which the value of g has not converged are printed; and the number of iterations needed for the integration, by which g values are calculated, are printed. Default is false at startup. Optionally, debug_diffuse_layer or -debug_d [ iffuse_layer ].
( True or False )--A value of true indicates the debugging information will be included in the output file; false indicates debugging information will not be printed. If neither true nor false is entered on the line, true is assumed. Optionally, t [ rue ] or f [ alse ].
Line 8: -debug_inverse [( True or False )]
-debug_inverse --Includes debugging prints for subroutines called by subroutine inverse_models . If this option is set to true , a large amount of information about the process of finding inverse models is printed. The program will print the following for each set of equations and inequalities that are attempted to be solved by the optimizing solver: a list of the unknowns, a list of the equations, the array that is to be solved, any nonnegativity or nonpositivity constraints on the unknowns, the solution vector, and the residual vector for the linear equations and inequality constraints. The printout is long and not very useful. Default is false at startup. Optionally, debug_inverse or -debug_i [ nverse ].
( True or False )--A value of true indicates the debugging information will be included in the output file; false indicates debugging information will not be printed. If neither true nor false is entered on the line, true is assumed. Optionally, t [ rue ] or f [ alse ].
Line 9: -debug_model [( True or False )]
-debug_model --Includes debugging prints for subroutines called by subroutine model . If this option is set to true , a large amount of information about the Newton-Raphson iterations is printed. The program will print some or all of the following at each iteration: the array that is solved, the solution vector calculated by the solver, the residuals of the linear equations and inequality constraints, the values of all of the master unknowns and their change, the moles of each pure phase and phase mole transfers, the moles of each element in the system minus the amount in pure phases and the change in this quantity. The printout is long and not very useful. If the numerical method does not converge in iterations -1 iterations (default is after 99 iterations), this printout is automatically begun and sent to the log file phreeqc.log . Default is false at startup. Optionally, debug_model or -debug_m [ odel ].
( True or False )--A value of true indicates the debugging information will be included in the output file; false indicates debugging information will not be printed. If neither true nor false is entered on the line, true is assumed. Optionally, t [ rue ] or f [ alse ].
Line 10: -debug_prep [( True or False )]
-debug_prep --Includes debugging prints for subroutine prep . If this option is set to true , the chemical equation and log K for each species and phase, as rewritten for the current calculation, are written to the output file. The printout is long and not very useful. Default is false at startup. Optionally, debug_prep or -debug_p [ rep ].
( True or False )--A value of true indicates the debugging information will be included in the output file; false indicates debugging information will not be printed. If neither true nor false is entered on the line, true is assumed. Optionally, t [ rue ] or f [ alse ].
Line 11: -debug_set [( True or False )]
-debug_set --Includes debugging prints for subroutines called by subroutine set . If this option is set to true , the initial revisions of the master unknowns (see equation 84, Parkhurst and Appelo, 1999), which occur in subroutine set, are printed for each element or element valence state that fails the initial convergence criteria. The initial revisions occur before the Newton-Raphson method is invoked and attempt to provide good estimates of the master unknowns to the Newton-Raphson method. Default is false at startup. Optionally, debug_set or -debug_s [ et ].
( True or False )--A value of true indicates the debugging information will be included in the output file; false indicates debugging information will not be printed. If neither true nor false is entered on the line, true is assumed. Optionally, t [ rue ] or f [ alse ].
Line 12: -logfile [( True or False )]
-logfile --Prints information to a file named phreeqc.log . If this option is set to true , information about each calculation will be written to the log file. The information includes the number of iterations in revising the initial estimates of the master unknowns, the number of Newton-Raphson iterations, and the iteration at which any infeasible solution was encountered while solving the system of nonlinear equations. (An infeasible solution occurs if no solution to the equality and inequality constraints can be found.) At each iteration, the identity of any species that exceeds 30 mol (an unreasonably large number) is written to the log file and noted as an “overflow”. Any basis switches are noted in the log file. The information about infeasible solutions and overflows can be useful for altering other parameters defined through the KNOBS data block, as described below. Default is false at startup. Optionally, logfile or -l [ ogfile ].
( True or False )--A value of true indicates log information will be written to the file, phreeqc.log ; false indicates log information will not be written. If neither true nor false is entered on the line, true is assumed. Optionally, t [ rue ] or f [ alse ].