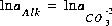(for the default database files) and 
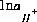. In this case, the pH will be calculated in the speciation calculation and will not be equal to the input pH.NUMERICAL METHOD FOR SPECIATION AND FORWARD MODELING
, 
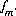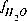, and 
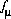, which are equations for mole balance for elements or element valence states, activity of water, and ionic strength. Mole-balance equations for hydrogen and oxygen are not included, because the total masses of hydrogen and oxygen generally are not known. Instead, the mass of water is assumed to be 1.0 kg and the total masses of hydrogen and oxygen are calculated after the speciation calculation has been completed. An additional mole-balance equation for alkalinity, 
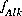, may be included to calculate 
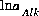and the total molality of the element associated with alkalinity (carbon in the default database). A charge-balance equation, 
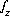, may be included to calculate the 
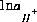that produces charge balance in the solution or a phase-equilibrium equation, 
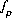, may be included to calculate 
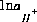that produces a target saturation index for the phase. In either of these last two cases, the pH of the solution is calculated and will not equal the input pH. A charge-balance equation, 
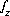, may be included to calculate the 
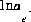that produces charge balance in the solution (not recommended) or a phase-equilibrium equation, 
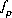, may be included to calculate 
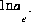that produces a target saturation index for the phase. In either of these last two cases, the pe of the solution is calculated and will not equal the input pe. A charge-balance equation, 
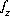, may be specified to replace a mole-balance equation, 
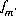, in which case, 
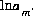is adjusted to produce charge balance for the solution. A phase-equilibrium equation, 
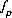may be specified to replace a mole-balance equation, 
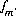, in which case, 
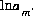is adjusted to produce a target saturation index for the phase. If a mole-balance equation is replaced by either the charge-balance equation or a phase-equilibrium equation, then the total amount of the element or valence state in the speciated solution will be calculated and will not equal the input concentration.
If the problem definition contains a mole-balance equation for both carbon [or carbon(+4)] and alkalinity, then the two master unknowns associated with these equations are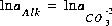
(for the default database files) and
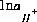. In this case, the pH will be calculated in the speciation calculation and will not be equal to the input pH.
For speciation calculations, if the alkalinity mole-balance equation is included in the problem formulation, it is included as the only optimization equation for the solver. All other equations are included as equality constraints. No inequality constraints are included for speciation calculations.
The redox options for aqueous speciation calculations are determined by the mass-action expressions used for aqueous species. By default, whenever a value of the activity of the electron is needed to calculate the molality or activity of an aqueous species, the input pe is used. If a default redox couple is given (-redox) or a redox couple is specified for an element (or combination of element valence states) (see SOLUTION keyword), then the mass-action expression for each aqueous species of the redox element is rewritten to remove the activity of the electron from the expression and replace it with the activities of the redox couple. For example, if iron (Fe) is to be distributed using the sulfate-sulfide redox couple [S(+6)/S(-2)], then the original chemical reaction for Fe+3:
(72) 
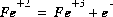
would be rewritten using the association reaction for sulfide,
(73) 
,
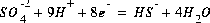to produce the following chemical reaction that does not include electrons:
(74) 
.
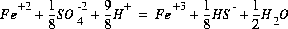The mass-action expression for this final reaction would be used as the mass-action expression for the species 
, and the differential for the change in the number of moles of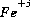 
, 
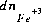, would also be based on this mass-action expression. However, the original mass-action expression (based on equation 72) is used to determine the mole-balance equations in which the term 
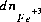appears, that is, the species 
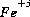would appear in the mole-balance equation for iron, but not in the mole-balance equations for S(+6) or S(-2).
By default, if a saturation-index calculation requires a value for pe (or activity of the electron), then the input pe is used. If a default redox couple has been defined (-redox), then the dissolution reaction for the phase is rewritten as above to eliminate the activity of the electron and replace it with the activities of the redox couple.
The set of master unknowns may change for redox elements during a calculation. The process, which is termed "basis switching", occurs if the activity of the master species which is the master unknown for a mole-balance equation becomes ten orders of magnitude smaller than the activity of another master species included in the same mole-balance equation. In this case, all of the mass-action expressions involving the current master unknown (including aqueous, exchange, gas, and surface species, and pure phases) are rewritten in terms of the new master species that has the larger activity. An example of this process is, if nitrogen is present in a system that becomes reducing, the master unknown for nitrogen would switch from nitrate, which would be present in negligible amounts under reducing conditions, to ammonium, which would be the dominant species. Basis switching does not affect the ultimate equilibrium distribution of species, but it does speed calculations and avoid numerical problems in dealing with small concentrations.
Initial values for the master unknowns are estimated and then revised according to the strategy described in the previous section. For initial solution calculations, the input values for pH and pe are used as initial estimates. The mass of water is 1.0 kg, and the activity of water is estimated to be 1.0. Ionic strength is estimated assuming the master species are the only species present and their concentrations are equal to the input concentrations (converted to units of molality). The activity of the master species of elements (except hydrogen and oxygen) and element valence states are set equal to the input concentration (converted to molality). If the charge-balance equation or a phase-equilibrium equation is used in place of the mole-balance equation for an element or element valence state, then the initial activity of the master species is set equal to one thousandth of the input concentration (converted to molality).
For data input to PHREEQC all options for a speciation calculation--use of an alkalinity equation; charge-balance equation; phase-equilibrium equation to adjust pH, or the concentrations of an element or an element valence state; and redox couples--are all defined in SOLUTION keyword data block. (See Description of Data Input.)