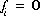, in unknowns 
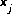the Newton-Raphson method involves iteratively revising an initial set of values for the unknowns. Let 
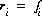be the residuals of the equations for the current values of the unknowns. The following set of equations is formulated:User's Guide to PHREEQC
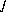in the previous sections. These include 
, 
, 
, 
, 
, 
, 
, 
, 
, 
, 
, 
, 
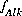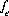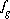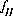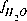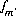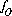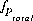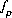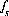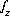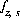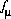, and 
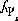, where 
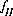and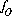 
are the simply the mole-balance functions for hydrogen and oxygen and 
refers to all aqueous master species except H+, e-, H2O and the alkalinity master species. The corresponding set of master unknowns is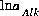 
, 
, 
, 
, 
, 
, 
, 
, 
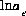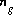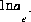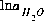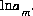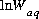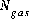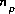(or possibly 
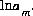in speciation calculations), 
, 
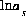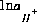(or possibly 
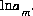in speciation calculations), 
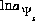(explicit diffuse-layer calculation), 
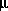, and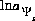 
(implicit diffuse-layer calculation). When the residuals of all the functions that are included for a given calculation are equal to zero, a solution to the set of nonlinear equations has been found, and the equilibrium values for the chemical system have been determined. (Note that some equations that are initially included in a given calculation may be dropped if a pure phase or gas phase does not exist at equilibrium.) The solution technique assigns initial values to the master variables and then uses a modification of the Newton-Raphson method iteratively to revise the values of the master variables until a solution to the equations has been found within specified tolerances.
For a set of equations,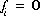
, in unknowns
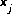the Newton-Raphson method involves iteratively revising an initial set of values for the unknowns. Let
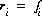be the residuals of the equations for the current values of the unknowns. The following set of equations is formulated:
(69) 
.
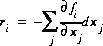The set of equations is linear and can be solved simultaneously for the unknowns,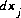 
. New values of the unknowns are calculated, 
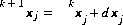, where k refers to the iteration number, after which, new values of the residuals are calculated. The process is repeated until the values of the residuals are less than a specified tolerance.
Two problems arise when using the Newton-Raphson method for chemical equilibria. The first is that the initial values of the unknowns must be sufficiently close to the equilibrium values, or the method does not converge, and the second is that a singular matrix may arise in problems involving multiple phases (if the number of phases exceeds the number allowed by the Gibbs' Phase Rule). PHREEQC uses an optimization technique developed by Barrodale and Roberts (1980) to solve the same Newton-Raphson equations, while avoiding some of the problems caused by singular matrices. The technique also allows inequality constraints to be added to the problem, which are useful for constraining the total amounts of phases that can react.
The selection of initial estimates for the master unknowns is described for each type of modeling in the following sections. Regardless of the strategy for assigning the initial estimates, the estimates for the activities of the master species for elements or element valence states are revised, if necessary, before the Newton-Raphson iterations to produce approximate mole balance. The procedure is as follows. After the initial estimates are made, the distribution of species is calculated and, for each element (except hydrogen and oxygen), element valence state, exchanger, and surface. Then, the ratio of the calculated number of moles to the input number of moles is calculated. If the ratio for a master species,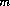 
, is greater than 1.5 or less than 10-5, then the following equation is used to revise the value of the master unknown:
(70) 
,
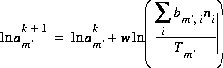where 
is 1.0 if the ratio is greater than 1.5 and 0.3 if the ratio is less than 10-5, and k is the iteration number. After revisions to the initial estimates, the distribution of species is calculated. The iterations continue until the ratios are within the specified ranges, at which point the modified Newton-Raphson technique is used.
The optimization technique of Barrodale and Roberts (1980) is a modification of the simplex linear programming algorithm that performs an L1 optimization (minimize sum of absolute values) on a set of linear equations subject to equality and inequality constraints. The general problem can be posed with the following matrix equations:
(71) 
.
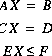The first matrix equation is minimized in the sense that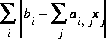 
is a minimum, where i is the index of rows and j is the index for columns, subject to the equality constraints of the second matrix equation and the inequality constraints of the third matrix equation.
The approach of PHREEQC is to include some of the Newton-Raphson equations (eq. 69) in the optimization equations (first matrix equation above), rather than include all of the Newton-Raphson equations as equalities (second matrix equation above). Equations that are included in the A matrix may not be solved for exact equality at a given iteration, but will be optimized in the sense given above. Thus, at a given iteration, an approximate mathematical solution to the set of Newton-Raphson equations can be found even if no exact equality solution exists, for example when direct application of the Newton-Raphson approach would result in unsolvable singular matrices.
After a solution to the equations, with equality and inequality constraints, is returned by the solver, the results, which are the size of the changes to the master unknowns, are checked to make sure that the values of the variables do not change too fast, as specified by default criteria in the program (or specified by the KNOBS keyword). If the criteria are not met, then the changes to the unknowns, except the mole transfers of pure phases, are decreased proportionately to satisfy all the criteria. Pure-phase mole transfers are not altered except to produce nonnegative values for the total moles of the pure phases. If all of the changes to the unknowns are small (as specified by convergence criteria within the program), the problem is solved. Otherwise, after suitable changes to the unknowns have been calculated, the master unknowns are updated, new molalities and activities of all the aqueous, exchange, and surface species are calculated, and residuals for all of the functions are calculated. The residuals are tested for convergence, and a new iteration is begun if convergence has not been attained.