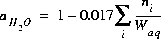.EQUATIONS FOR SPECIATION AND FORWARD MODELING
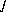, are defined in this section. These functions describe heterogeneous equilibrium and are derived primarily by substituting the equations for the number of moles of species (derived from mass-action equations in the previous section) into mole- and charge-balance equations. Each function is presented along with the total derivative with respect to the master unknowns.
(18)
.
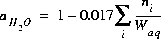The function,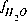 
, is defined as follows:
(19) 
,
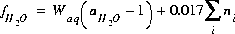and the total derivative of this function is
(20) 
,
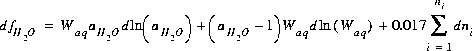The master unknown is the natural log of the activity of water.
(21) 
.
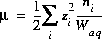The function,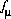 
, is defined as follows:
(22) 
,
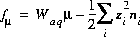and the total derivative of this function is
(23) 
.
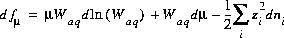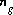.A mass-action equation is used to relate gas-component activities (fugacities) to aqueous phase activities. PHREEQC uses dissolution equations, in the sense that the gas component is assumed to be on the left-hand side of the chemical reaction. For carbon dioxide, the dissolution reaction may be written as follows:
(24) 
.
The Henry's law constant relates the partial pressure of the gas component to the activity of aqueous species. For carbon dioxide, the Henry's law constant is 10-1.468, and the following mass-action equation obtains at equilibrium:
(25) 
,
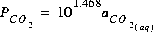where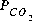 
is the partial pressure calculated using activities in the aqueous phase. In general, the partial pressure of a gas component may be written in terms of aqueous phase activities as follows:
(26) 
,
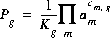where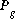 
is the partial pressure of gas component g, calculated using activities in the aqueous phase; 
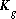is the Henry's law constant for the gas component; and 
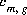is the stoichiometric coefficient of master species, m, in the dissolution equation. The values of 
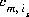may be positive or negative. For PHREEQC, terms on the left-hand side of a dissolution reaction are assigned negative coefficients and terms on the right-hand side are assigned positive coefficients.
At equilibrium, the number of moles of a gas component in the gas phase is equal to the partial pressure of the gas times the total number of moles of gas in the gas phase,
(27) 
.
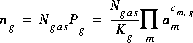The total derivative of the number of moles of a gas component in the gas phase is
(28) 
.
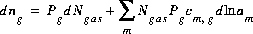For mole-balance equations, the numerical model treats the gas phase components in the same way that it treats aqueous species. Thus, the terms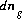 
appear in the Jacobian for the mole-balance equations for each element. The total number of moles of each element in the system includes both the number of moles in the gas phase and the number of moles in the aqueous phase.
Apart from the new terms in mole-balance equations, the one new function for the gas phase requires that the sum of the partial pressures of the component gases is equal to the total pressure, Ptotal. The function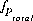 
is defined as follows:
(29) 
.
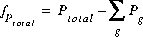The total derivative of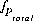 
with respect to the master unknowns, with the convention that positive dNgas are increases in solution concentration, is
(30) 
.
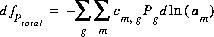For data input to PHREEQC, the mass-action equations, Henry's law constant, and temperature dependence of the constant for gas phases are defined with the PHASES keyword data block. Components to include in gas-phase calculations and initial gas composition are defined with the GAS_PHASE keyword data block. (See Description of Data Input.)
The new function corresponding to each of the new unknowns is a mass-action expression for each pure phase. PHREEQC uses dissolution reactions, in the sense that the pure phase is on the left-hand side of the chemical equation. For calcite, the dissolution reaction may be written as
(31) 
,
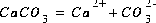and, using log K of 10-8.48 and activity of the pure solid is 1.0, the resulting mass-action expression is
(32) 
.
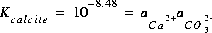In general, pure-phase equilibria can be represented with the following equation:
(33) 
,
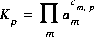where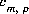 
is the stoichiometric coefficient of master species, m, in the dissolution reaction. The values of 
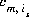may be positive or negative. For PHREEQC, terms on the left-hand side of a dissolution reaction are assigned negative coefficients and terms on the right-hand side are assigned positive coefficients. The saturation index for the mineral, SIp, is defined to be
(34) 
.
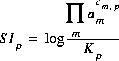The function used for phase equilibrium in the numerical method is
(35) 
,
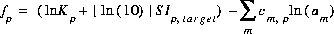where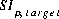 
is a specified target saturation index for the phase (see keyword EQUILIBRIUM_PHASES) and 
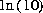converts base-10 log to natural log. For single-component gas phases, 
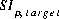is equivalent to the log of the partial pressure of the gas. The total derivative with respect to the master unknowns is
(36) 
.
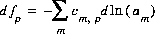For data input to PHREEQC, the mass-action equations, equilibrium constant, and temperature dependence of the constant for pure phases are defined with the PHASES keyword data block. Initial composition of a pure-phase assemblage is defined with the EQUILIBRIUM_PHASES keyword data block. (See Description of Data Input.)
(37) 
,
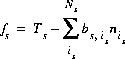where the value of the function, fs, is zero when mole balance is achieved, Ts is the number of equivalents surface site s, and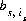 
is the number of surface sites occupied by the surface complex. The total derivative of fs is
(38) 
.
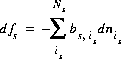For data input to PHREEQC, the number of moles of each type of surface site is defined with the SURFACE keyword data block. Surface species are defined with the SURFACE_SPECIES keyword data block. (See Description of Data Input.)
(39) 
,
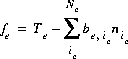where, the value of the function, fe, is zero when mole balance is achieved, Te is the total number of exchange sites for exchanger 
, and 
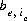is the number of exchange sites occupied by the exchange species. The total derivative of fe is
(40) 
.
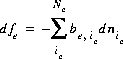For data input to PHREEQC, the number of moles of exchange sites is defined in the EXCHANGE keyword data block. Exchange species are defined with the EXCHANGE_SPECIES data block. (See Description of Data Input.)
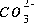. The master unknown for alkalinity is 
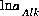, or for the default databases, 
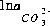.The total number of equivalents of alkalinity is specified by input to the model. The sum of the alkalinity contribution of each aqueous species must equal the total number of equivalents of alkalinity. The following function is derived from the alkalinity-balance equation:
(41) 
,
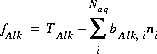where, the value of the function, fAlk, is zero when mole balance is achieved, TAlk is the number of equivalents of alkalinity in solution, and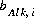 
is alkalinity contribution of the aqueous species, eq/mol. The total derivative of fAlk is
(42) 
.
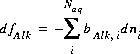The value of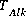 
may be positive or negative. Conceptually, a measured alkalinity differs from the alkalinity calculated by PHREEQC. In the default database files for PHREEQC the values of 
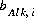have been chosen such that the reference state (
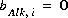) for each element or element valence state is the predominant species at a pH of 4.5. It is assumed that all of the element or element valence state is converted to this predominant species in a theoretical alkalinity titration. However, in a real alkalinity titration, significant concentrations of species of elements and element valence states that have nonzero alkalinity contributions may exist at the endpoint of the titration, and the extent to which this occurs causes the alkalinity calculated by PHREEQC to be a different quantity than the measured alkalinity. Species that are especially susceptible to this problem are the hydroxide complexes of iron and aluminum. Thus, the alkalinity of a solution as calculated by PHREEQC, though it will be numerically equal to the measured alkalinity, is necessarily an approximation because of the assumption that a titration totally converts elements and element valence states to their reference state. In most solutions, where the alkalinity is derived predominantly from carbonate species, the approximation is valid.
For data input to PHREEQC, the alkalinity of each species is calculated from the association reaction for the species, which is defined in the SOLUTION_SPECIES keyword data block, and the alkalinity contributions of the master species, which are defined with the SOLUTION_MASTER_SPECIES keyword data block. Total alkalinity is part of the solution composition defined with the SOLUTION keyword data block. (See Description of Data Input.)
(43) 
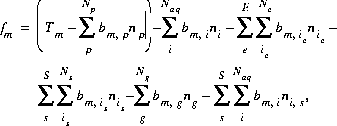
where the value of the function, fm, is zero when mole-balance is achieved. Tm is the total number of moles of the element in the system. E is the number of exchangers in the exchange assemblage, S is the number of surfaces in the surface assemblage. Np is the number of phases in the pure-phase assemblage, Naq is the number of aqueous species, Ne is the number of exchange species for exchanger e, Ns is the number of surface species for surface s, and Ng is the number of gas components. The number of moles of each entity in the system is represented by np for phases in the pure-phase assemblage, ni for aqueous species,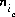 
for the exchange species of exchanger e, 
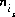for surface species for surface s, ng for the gas components, and 
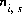for the aqueous species in the diffuse layer of surface s. The number of moles of element, m, per mole of each entity is represented by bm, with an additional subscript to define the relevant entity; 
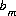is usually, but not always, equal to 
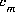(the coefficient of the master species for m in the mass-action equation), except for elements hydrogen and oxygen.
To avoid solving for small differences between large numbers, the quantity in parenthesis in the previous function is not explicitly included in the solution algorithm and the value of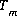 
is never actually calculated. Instead the quantity 
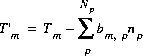is used in the function 
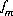. Initially, 
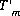is calculated from the total concentration of 
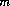in the aqueous phase, the exchange assemblage, the surface assemblage, and the gas phase:
(44) 
.
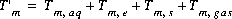During the iterative solution to the equations,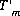 
is updated by the mole transfers of the pure phases:
(45) 
,
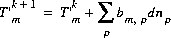where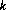 
refers to the iteration number. It is possible for 
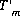to be negative in intermediate iterations, but must be positive when equilibrium is attained.
The total derivative of the function, fm, is
(46) 
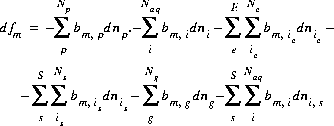
For data input to PHREEQC, total moles of elements are defined initially through keyword data input and speciation, initial exchange, and initial surface calculations. Moles of elements are initially defined for an aqueous phase (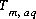
) with the SOLUTION keyword data block, for an exchange assemblage (
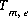) with the EXCHANGE keyword data block, for a surface assemblage (
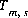) with the SURFACE keyword data block, for the gas phase (
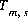) with a GAS_PHASE keyword data block. The number of moles of each phase in a pure phase assemblage (
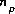) is defined with the EQUILIBRIUM_PHASES keyword data block. Total moles of elements and total moles of pure phases may be modified by reaction calculations. (See Description of Data Input.)
In real solutions, the sum of the equivalents of anions and cations must be zero. However, analytical errors and unanalyzed constituents in chemical analyses generally cause electrical imbalances to be calculated for solutions. If a charge imbalance is calculated for an initial solution, the pH is adjusted in subsequent reaction or transport simulations to maintain the same charge imbalance. If mixing is performed, the charge imbalance for the reaction step is the sum of the charge imbalances of each solution weighted by its mixing factor. If a surface is used in a simulation and the explicit diffuse-layer calculation is not specified, then the formation of charged surface species will result in a charged surface. Similarly, if exchange species are not electrically neutral (all exchange species in the default database are electrically neutral), the exchanger will accumulate a charge. These charge imbalances must be included in the charge-balance equation to calculate the correct pH in reaction and transport simulations. In general, the charge imbalance for a solution is calculated at the end of the initial solution calculation and at the end of each reaction and transport simulation with the following equation:
(47) 
,
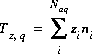where zi is the charge on the aqueous species and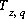 
is the charge imbalance for aqueous phase q. If charged surfaces or exchangers are not present, the charge imbalance for a solution at the end of a simulation will be the same as at the beginning of the simulation.
The charge imbalance on a surface is calculated at the end of the initial surface calculation and at the end of each reaction and transport simulation with the following equation:
(48) 
,
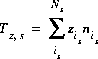where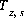 
is the charge imbalance for the surface, and 
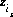is the charge on the surface species i of surface s. If the composition of the diffuse layer is explicitly included in the calculation (-diffuse_layer in the SURFACE keyword data block), then each solution should be charge balanced using one of the charge balance options, and 
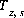will equal to zero.
Normally, exchange species have no net charge, but for generality, this is not required. However, the activity of exchange species (the equivalent fraction) is not well defined if the sum of the charged species is not equal to the total number of equivalents of exchange sites (exchange capacity). If charged exchange species exist, then the charge imbalance on an exchanger is calculated at the end of the initial exchange calculation and at the end of each reaction and transport simulation with the following equation:
(49) 
,
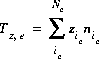where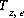 
is the charge imbalance for the exchanger, and 
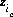is the charge on the exchange species i of exchanger e.
The charge imbalance for the system is defined at the beginning of each reaction or transport simulation with the following equation:
(50) 
,
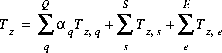where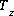 
is the charge imbalance for the system, Q is the number of aqueous phases that are mixed in the reaction or transport step, 
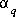is the mixing fraction for aqueous phase q.
The charge-balance function is
(51) 
,
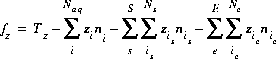where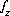 
is zero when charge balance has been achieved and the double summation for surfaces is present only if the diffuse-layer composition is not explicitly calculated. The total derivative of 
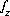is
(52) 
,
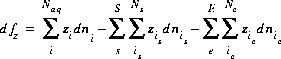and, again, the double summation for surfaces is present only if the diffuse-layer composition is not explicitly calculated.
For data input to PHREEQC, charge imbalance is defined by data input for SOLUTION, EXCHANGE, and SURFACE keyword data blocks combined with speciation, initial exchange, and initial surface calculations. The charge on a species is defined in the balanced chemical reaction that defines the species in SOLUTION_SPECIES, EXCHANGE_SPECIES, or SURFACE_SPECIES keyword data blocks. (See Description of Data Input.)
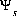. The surface-charge density is the amount of charge per area of surface material, which can be calculated from the distribution of surface species as follows:
(53) 
,
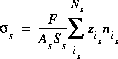where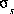 
is the charge density for surface s in coulombs per square meter (C/m2), F is the Faraday constant in coulomb per mole (96,485 C/mol), As is the specific area of the surface material (m2/g), and Ss is the mass of surface material (g). At 25oC, the surface-charge density is related to the electrical potential at the surface by the following equation involving the hyperbolic sine:
(54) 
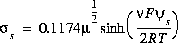
where 
is the valence of a symmetric electrolyte,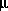 
is the ionic strength, F is the Faraday constant in kilojoules per volt-equivalent (kJ V-1 eq-1, which equals C/mol), 
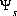is the potential at the surface in volts, R is the gas constant (8.314 J mol-1 oK-1), and T is in Kelvin. The following assumptions apply to equation 54: (1) Although strictly valid only at 25oC, the constant 0.1174 is used at all temperatures, and (2) the valence of the electrolyte is assumed to be 1. See the following sections, Surface Charge-Potential Equation with Explicit Calculation of the Diffuse-Layer Composition and Non-Electrostatic Surface-Complexation Modeling, for alternate formulations of surface-complexation modeling.
The charge-potential function is defined as follows:
(55) 
,
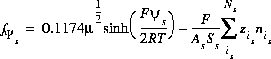and the total derivative of this function is
(56) 
.
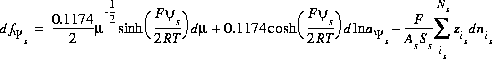For data input to PHREEQC, calculation without an explicit diffuse layer is the default. Specific surface area (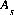
) and mass of surface (
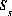) are defined in the SURFACE keyword data block. The charge on a surface species is defined in the balanced chemical reaction that defines the species in the SURFACE_SPECIES keyword data block. (See Description of Data Input.)
The surface excess is defined to be
(57) 
,
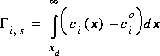where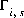 
is the surface excess in mol m-2, 
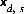is the location of the outer Helmholtz plane, 
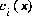is concentration as a function of distance from the surface in mol m-3, and 
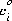is the concentration in the bulk solution. The surface excess is related to concentration in the reference state of 1.0 kg of water,
(58) 
,
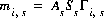where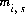 
is the surface excess of aqueous species i in mol/kg water. This surface-excess concentration can be related to the concentration in the bulk solution by
(59) 
,
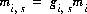where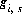 
is a function of the potential at the surface and the concentrations and charges of all ions in the bulk solution:
(60) 
,
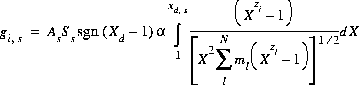where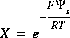 
, 
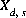is the value at the outer Helmholtz plane, and 
, 
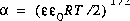is the dielectric constant for water, 78.5 (unitless), and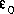 
is the dielectric permittivity of a vacuum, 8.854x10-12 C V-1 m-1. The value of 
at 25oC is 0.02931 [(L/mol)1/2 C m-2, where L is liters, mol is moles, C is coulombs, and m is meters]. The relation between the unknown (X) used by Borkovec and Westall (1983) and the master unknown used by PHREEQC is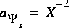 
.
The development of Borkovec and Westall (1983) calculates only the total excess concentration in the diffuse layer of each aqueous species. A problem arises in reaction and transport modeling when a solution is removed from the surface, for example, in an advection simulation when the water in one cell advects into the next cell. In this case, the total number of moles that remain with the surface needs to be known. In PHREEQC, an arbitrary assumption is made that the diffuse layer is a specified thickness and that all of the surface excess resides in the diffuse layer. The total number of moles of an aqueous species in the diffuse layer is then the sum of the contribution from the surface excess plus the bulk solution in the diffuse layer:
(61) 
,
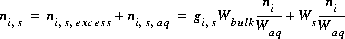where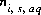 
refers to the number of moles of aqueous species i that is present in the diffuse layer due to the contribution from the bulk solution, 
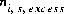refers to the number of moles that is added to the diffuse layer due to the surface excess calculation, 
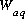is the mass of water in the system excluding the diffuse layer, 
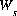is the mass of water in the diffuse layer of surface s, and 
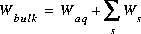. The mass of water in the diffuse layer is calculated from the thickness of the diffuse layer and the surface area, assuming 1 L contains 1 kg water:
(62) 
,
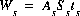where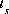 
is the thickness of the diffuse layer in meters.
The total derivative of the number of moles of an aqueous species in the diffuse layer is as follows:
(63) 
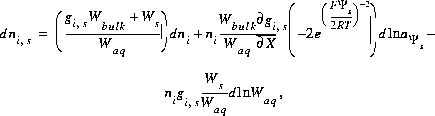
where the second term is the partial derivative with respect to the master unknown for the potential at the surface,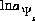 
. The partial derivative, 
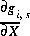, is equal to the integrand from equation 60 evaluated at 
:
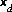(64) 
,
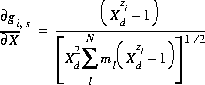and the partial derivative of the function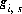 
with respect to the master unknown is
(65) 
.
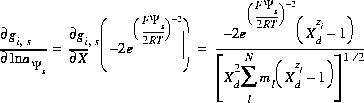In the numerical method, it is computationally expensive to calculate the functions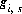 
, so the same approach as Borkovec and Westall (1983) is used in PHREEQC to reduce the number of function evaluations. A new level of iterations is added when the diffuse layer is explicitly included in the calculations. The functions and their partial derivatives are explicitly evaluated once at the beginning of each of these diffuse-layer iterations. During the model iterations, which occur within the diffuse-layer iterations, the values of the functions are updated using the following equation:
(66) 
,
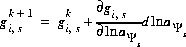where k refers to the model iteration number and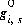 
is the value that is evaluated explicitly at the beginning of the diffuse-layer iteration. The model iterations end when the Newton-Raphson method has converged on a solution, however, convergence is based on the values of the functions 
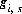that are estimates. Thus, diffuse-layer iterations must continue until the values of the functions have converged within specified tolerances, that is, the changes in the values of the functions are small between one diffuse-layer iteration and the next.
When explicitly calculating the composition of the diffuse layer, the function involving the sinh of the potential unknown (equation 54) is replaced with a charge-balance function that includes the surface charge and the diffuse-layer charge:
(67) 
,
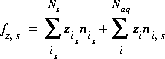where, the value of the function,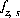 
, is zero when charge balance is achieved. The total derivative of the function, 
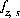, is
(68) 
.
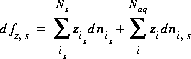For data input to PHREEQC, explicit calculation of the diffuse layer is invoked using the -diffuse_layer identifier in the SURFACE keyword data block. Specific surface area (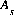
) and mass of surface (
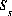) are also defined in the SURFACE keyword data block. The charge on a surface species or an aqueous species is defined in the balanced chemical reaction that defines the species in the SURFACE_SPECIES or SOLUTION_SPECIES keyword data block. (See Description of Data Input.)
For data input to PHREEQC, the non-electrostatic model for a surface is invoked by using the -no_edl identifier in the SURFACE keyword data block. (See Description of Data Input.)