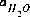 , the ionic strength,
, the ionic strength, 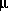 , and the mass of solvent water in an aqueous solution, Waq.
, and the mass of solvent water in an aqueous solution, Waq. EQUATIONS FOR SPECIATION AND FORWARD MODELING
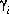 , molality, mi, and number of moles in solution, ni, of each aqueous species, i. The following relationships apply to all aqueous species (except aqueous electrons and water itself):
, molality, mi, and number of moles in solution, ni, of each aqueous species, i. The following relationships apply to all aqueous species (except aqueous electrons and water itself): 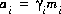 and
and 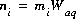 , where
, where 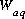 is the mass of water in the aqueous phase.
is the mass of water in the aqueous phase.
PHREEQC rewrites all chemical equations in terms of master species. There is one master aqueous species associated with each element (for example, Ca+2 for calcium) or element valence state (for example, Fe+3 for ferric iron) plus the activity of the hydrogen ion, the activity of the aqueous electron, and the activity of water. For PHREEQC, the identity of each aqueous master species is defined with SOLUTION_MASTER_SPECIES keyword data block. (See Description of Data Input.) The numerical method reduces the number of unknowns to be a minimum number of master unknowns, and iteratively refines the values of these master unknowns until a solution to the set of algebraic equations is found. The master unknowns for aqueous solutions are the natural log of the activities of master species, the natural log of the activity of water, 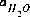 , the ionic strength,
, the ionic strength, 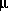 , and the mass of solvent water in an aqueous solution, Waq.
, and the mass of solvent water in an aqueous solution, Waq.
Equilibrium among aqueous species in an ion-association model requires that all mass-action equations for aqueous species are satisfied. For example, the association reaction for the aqueous species 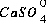 is
is 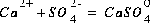 . The log K for this reaction at 25oC is 2.3, which results in the following mass-action equation:
. The log K for this reaction at 25oC is 2.3, which results in the following mass-action equation:
(1) 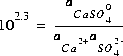 .
.
In general, mass-action equations can be written as follows:
(2) 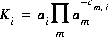 ,
,
where cm,i is the stoichiometric coefficient of master species m in species i. The values of cm,i may be positive or negative. For PHREEQC, terms on the right-hand side of an association reaction are assigned negative coefficients and terms on the left-hand side are assigned positive coefficients. Ki is an equilibrium constant that is dependent on temperature, and m ranges over all master species. The same formalism applies to master species, where the mass-action equation is simply 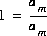 .
.
For aqueous species the equation, derived from the mass-action expression, for the total number of moles of species i is
(3) 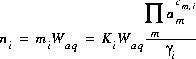 .
.
The Newton-Raphson method uses the total derivative of the number of moles with respect to the master unknowns. The total derivative is
(4) 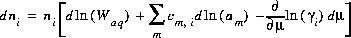 .
.
Activity coefficients of aqueous species are defined with the following equations:
(5) 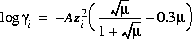 ,
,
which is referred to as the Davies equation, or
(6) 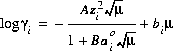 ,
,
which is referred to as either the extended Debye-Hückel equation, if bi is zero, or the WATEQ Debye-Hückel equation (see Truesdell and Jones, 1974), if bi is not equal to zero. A and B are constants dependent only on temperature, 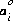 is the ion-size parameter in the extended Debye-Hückel equation,
is the ion-size parameter in the extended Debye-Hückel equation, 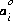 and bi are ion-specific parameters fitted from mean-salt activity-coefficient data in the WATEQ Debye-Hückel equation, and zi is the ionic charge of aqueous species i. Unless otherwise specified in the database file or the input data set, the Davies equation is used for charged species. For uncharged species, the first term of the activity coefficient equation is zero, and unless otherwise specified bi is assumed to be 0.1 for all uncharged species.
and bi are ion-specific parameters fitted from mean-salt activity-coefficient data in the WATEQ Debye-Hückel equation, and zi is the ionic charge of aqueous species i. Unless otherwise specified in the database file or the input data set, the Davies equation is used for charged species. For uncharged species, the first term of the activity coefficient equation is zero, and unless otherwise specified bi is assumed to be 0.1 for all uncharged species.
The partial derivatives of these activity coefficient equations with respect to ionic strength are
(7) 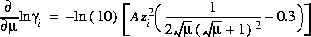 ,
,
for the Davies equation and
(8) 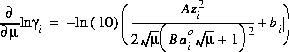 ,
,
for the extended or WATEQ Debye-Hückel equation.
For data input to PHREEQC, the chemical equation for the mole-balance and mass-action expression, the log K and its temperature dependence, and the activity coefficient parameters for each aqueous species are defined through the SOLUTION_SPECIES keyword data block. Master species for elements and element valence states are defined with the SOLUTION_MASTER_SPECIES keyword data block. Composition of a solution is defined with the SOLUTION keyword data block. (See Description of Data Input.)
The unknowns for exchange calculations are the activity, 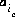 , which is defined to be the equivalent fraction in PHREEQC, and the number of moles,
, which is defined to be the equivalent fraction in PHREEQC, and the number of moles, 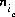 , of each exchange species,
, of each exchange species, 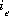 , of exchanger e. The equivalent fraction is the number of moles of sites occupied by an exchange species divided by the total number of exchange sites. The activity of an exchange species is defined as follows:
, of exchanger e. The equivalent fraction is the number of moles of sites occupied by an exchange species divided by the total number of exchange sites. The activity of an exchange species is defined as follows: 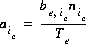 , where
, where 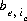 is the number of equivalents of exchanger, e, occupied by the exchange species,
is the number of equivalents of exchanger, e, occupied by the exchange species, 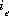 and
and 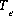 is the total number of exchange sites for the exchanger, in equivalents. Note that
is the total number of exchange sites for the exchanger, in equivalents. Note that 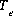 is the total number of equivalents of the exchanger in the system which is not necessarily equal to the number of equivalents per kilogram of water (eq/kg H2O), because the mass of water in the system may be more or less than 1 kg.
is the total number of equivalents of the exchanger in the system which is not necessarily equal to the number of equivalents per kilogram of water (eq/kg H2O), because the mass of water in the system may be more or less than 1 kg.
Equilibrium among aqueous and exchange species requires that all mass-action equations for the exchange species are satisfied. The association reaction for the exchange species 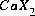 is
is 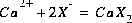 , where
, where 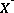 is the exchange master species for the default database. The use of equivalent fractions for activities and this form for the chemical reaction is known as the Gaines-Thomas convention (Gaines and Thomas, 1953) and is the convention used in the default database for PHREEQC. [It is also possible to use the Gapon convention in PHREEQC, which uses equivalent fraction, but writes the exchange reaction as
is the exchange master species for the default database. The use of equivalent fractions for activities and this form for the chemical reaction is known as the Gaines-Thomas convention (Gaines and Thomas, 1953) and is the convention used in the default database for PHREEQC. [It is also possible to use the Gapon convention in PHREEQC, which uses equivalent fraction, but writes the exchange reaction as 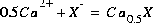 . See Appelo and Postma (1993) for more discussion.] The log K for calcium exchange in the default database file is 0.8, which results in the following mass-action equation:
. See Appelo and Postma (1993) for more discussion.] The log K for calcium exchange in the default database file is 0.8, which results in the following mass-action equation:
(9) 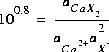 .
.
In general, mass-action equations can be written as follows:
(10) 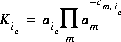 ,
,
where m varies over all master species, including exchange master species, 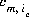 is the stoichiometric coefficient of master species, m, in the association half reaction for exchange species ie. The values of
is the stoichiometric coefficient of master species, m, in the association half reaction for exchange species ie. The values of 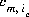 may be positive or negative. For PHREEQC, terms on the right-hand side of an association reaction are assigned negative coefficients and terms on the left-hand side are assigned positive coefficients.
may be positive or negative. For PHREEQC, terms on the right-hand side of an association reaction are assigned negative coefficients and terms on the left-hand side are assigned positive coefficients. 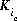 , is a half-reaction selectivity constant.
, is a half-reaction selectivity constant.
For an exchange species, the equation for the total number of moles of species ie is
(11) 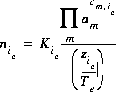 .
.
The natural log of the activity of the master species of the exchanger is an additional master unknown in the numerical method. The total derivative of the number of moles of species ie with respect to the master unknowns is
(12) 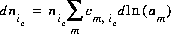 .
.
For data input to PHREEQC, the chemical equation for the mole-balance and mass-action expression and the log K and its temperature dependence for each exchange species are defined through the EXCHANGE_SPECIES keyword data block. Exchange master species are defined with the EXCHANGE_MASTER_SPECIES keyword data block. Number of exchange sites and exchanger composition are defined with the EXCHANGE keyword data block. (See Description of Data Input.)
The basic theory for surface-complexation reactions including electrostatic potentials is presented in Dzombak and Morel (1990). The theory assumes that the number of active sites, Ts (equivalents, eq), the specific area, As (meters squared per gram, m2/g), and the mass, Ss (g), of the surface are known. The activity of a surface species is assumed to be equal to its molality (moles of surface species per kilogram of water, even though surface species are conceptually in the solid phase). The two additional master unknowns are (1) the quantity, 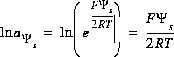 , where F is the Faraday constant,
, where F is the Faraday constant, 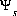 is the potential at surface s, R is the gas constant, and T is temperature in Kelvin and (2) the natural log of the activity of the master surface species. The identity of the master surface species is defined with SURFACE_MASTER_SPECIES keyword data block. (See Description of Data Input.) Note that the quantity
is the potential at surface s, R is the gas constant, and T is temperature in Kelvin and (2) the natural log of the activity of the master surface species. The identity of the master surface species is defined with SURFACE_MASTER_SPECIES keyword data block. (See Description of Data Input.) Note that the quantity 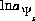 is defined with a 2 in the denominator of the term on the right hand side. This is a different master unknown than that used in Dzombak and Morel (1990), but produces the same results as their model because all equations are written to be consistent with this master unknown.
is defined with a 2 in the denominator of the term on the right hand side. This is a different master unknown than that used in Dzombak and Morel (1990), but produces the same results as their model because all equations are written to be consistent with this master unknown.
If "HfoOH" is used to represent a neutral surface-complexation site ("Hfo", Hydrous ferric oxide, is used in the default database files), the association reaction for the formation of a negatively charged site (it is an association reaction in the sense that the defined species is on the right hand side of the equation) can be written as follows:
(13) 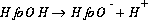 ,
,
and the mass-action expression including the electrostatic potential term is
(14) 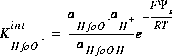 ,
,
where 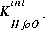 is the intrinsic equilibrium constant for the reaction,
is the intrinsic equilibrium constant for the reaction, 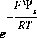 is a factor that accounts for the work involved in moving a charged species (H+) away from a charged surface. In general, the equation for surface species is is
is a factor that accounts for the work involved in moving a charged species (H+) away from a charged surface. In general, the equation for surface species is is
(15) 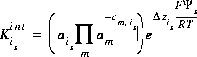 ,
,
where is is the ith surface species for surface s, m varies over all master species, including surface master species, 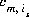 is the stoichiometric coefficient of master species, m, in the association half reaction for surface species is. The values of
is the stoichiometric coefficient of master species, m, in the association half reaction for surface species is. The values of 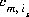 may be positive or negative. For PHREEQC, terms on the right-hand side of an association reaction are assigned negative coefficients and terms on the left-hand side are assigned positive coefficients.
may be positive or negative. For PHREEQC, terms on the right-hand side of an association reaction are assigned negative coefficients and terms on the left-hand side are assigned positive coefficients. 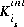 , is the intrinsic equilibrium constant, and
, is the intrinsic equilibrium constant, and 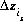 is the net change in surface charge due to the formation of the surface species.
is the net change in surface charge due to the formation of the surface species.
For a surface species, the equation for the total number of moles of species is is
(16) 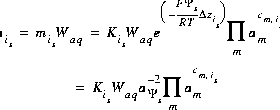 .
.
The total derivative of the number of moles of species is with respect to the master unknowns is
(17) 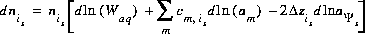 .
.
The second formulation of mass-action equations for surface species excludes the electrostatic potential term in the mass-action expression (-no_edl identifier in the SURFACE keyword data block). The equation for the number of moles of a surface species is the same as equation 16, except the factor involving 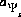 does not appear. Likewise, the total derivative of the number of moles is the same as equation 17, except the final term is absent.
does not appear. Likewise, the total derivative of the number of moles is the same as equation 17, except the final term is absent.
For data input to PHREEQC, the chemical equation for the mole-balance and mass-action expression and the log K and its temperature dependence of surface species are defined through the SURFACE_SPECIES keyword data block. Surface master species or types of surface sites are defined with the SURFACE_MASTER_SPECIES keyword data block. The number of sites, the composition of the surface, the specific surface area, and the mass of the surface are defined with the SURFACE keyword data block. (See Description of Data Input.)