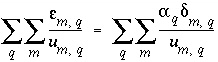). Next, a sum of the adjustment to each element concentration and isotopic com-This example repeats the inverse modeling calculations of the chemical evolution of spring-water compositions in the Sierra Nevada that are described in a classic paper by Garrels and Mackenzie (1967). The same example is described in the manual for the inverse-modeling program NETPATH (Plummer and others, 1991 and 1994). The example uses two spring-water compositions, one from an ephemeral spring, which is less chemically evolved, and one from a perennial spring, which probably has had a longer residence time in the subsoil. The differences in composition between the ephemeral and perennial spring are assumed to be due to reactions between the water and the minerals and gases it contacts. The object of inverse modeling in this example is to find sets of minerals and gases that, when reacted in appropriate amounts, quantitatively account for the differences in composition between the solutions.
NETPATH (Plummer and others 1991, 1994) and PHREEQC are both capable of performing inverse-modeling calculations. NETPATH has two advantages relative to PHREEQC: (1) NETPATH provides a thorough treatment of isotopes, including isotopic mole balance, isotope fractionation, and carbon-14 dating, whereas PHREEQC has only isotope mole-balance capabilities, and (2) NETPATH provides a completely interactive environment for data entry and model development, whereas PHREEQC (version 2) is primarily a batch-oriented program. On the other hand, complete graphical user interfaces are available for PHREEQC version 1, which lacks the isotope mole-balance capabilities (Charlton and others, 1997) and for version 2 (PHREEQC for Windows, V.E.A. Post, written commun., 1999, http://www.geo.vu.nl/users/posv/phreeqc.html ). The major advantage of inverse modeling with PHREEQC relative to NETPATH is the capability to include uncertainties in the analytical data that are used in the calculation of inverse models. This capability produces inverse models that are more robust, that is, small changes in input data do not produce large differences in model-calculated mole transfers. Another advantage of PHREEQC is that any set of elements may be included in the inverse-modeling calculations, whereas NETPATH is limited to a selected, though relatively comprehensive, set of elements.
The analytical data for the two springs are given in table 46. The chemical compositions of minerals and gases postulated to react by Garrels and Mackenzie (1967) and their mole transfers are given in table 47. The selection of the identity and composition of the reactive phases is the most difficult part of inverse modeling. In general the selection is made by knowledge of the flow system and the mineralogy along the flow path; microscopic and chemical analysis of the aquifer material and isotopic composition of the water and minerals provide additional insight for the selection of reactants. It is not necessary to know precisely which minerals are reacting, but it is necessary to have a comprehensive list of potential reactants.
The input data set for this example is given in table 48. The SOLUTION_SPREAD data block is used to define the two spring waters. The INVERSE_MODELING data block is used to define all of the characteristics of the inverse-modeling calculations, including the solutions and phases to be used, the mole-balance equations, the uncertainty limits, whether all or only "minimal" models will be printed, and whether ranges of mole transfer that are consistent with the uncertainty limits will be calculated. A series of identifiers (sub-keywords preceded by a hyphen) specify the characteristics of the inverse model.
Table 48. --Input data set for example 16
TITLE Example 16.--Inverse modeling of Sierra springs
SOLUTION_SPREAD
-units mmol/L
# "\t" indicates tab
Number\t pH\t Si\t Ca\t Mg\t Na\t K\t Alkalinity\t S(6)\t Cl
1\t 6.2\t 0.273\t 0.078\t 0.029\t 0.134\t 0.028\t 0.328\t 0.01\t 0.014
2\t 6.8\t 0.41 \t 0.26 \t 0.071\t 0.259\t 0.04 \t 0.895\t 0.025\t 0.03
INVERSE_MODELING 1
-solutions 1 2
-uncertainty 0.025
-balances
Ca 0.05 0.025
-phases
Halite
Gypsum
Kaolinite precip
Ca-montmorillonite precip
CO2(g)
Calcite
Chalcedony precip
Biotite dissolve
Plagioclase dissolve
-range
PHASES
Biotite
KMg3AlSi3O10(OH)2 + 6H+ + 4H2O = K+ + 3Mg+2 + Al(OH)4- + 3H4SiO4
log_k 0.0 # No log_k, Inverse modeling only
Plagioclase
Na0.62Ca0.38Al1.38Si2.62O8 + 5.52 H+ + 2.48H2O =\
0.62Na+ + 0.38Ca+2 + 1.38Al+3 + 2.62H4SiO4
log_k 0.0 # No log_k, Inverse modeling only
END
The identifier -solutions selects the solutions to be used by solution number. Two or more solution numbers must be listed after the identifier. If only two solution numbers are given, the second solution is assumed to evolve from the first solution. If more than two solution numbers are given, the last solution listed is assumed to evolve from a mixture of the preceding solutions. The solutions to be used in inverse modeling are defined in the same way as any solutions used in PHREEQC models. Usually the analytical data are entered in a SOLUTION or SOLUTION_SPREAD data block, but solutions defined by batch-reaction calculations in the current or previous simulations may also be used if they are saved with the SAVE keyword.
The -uncertainty identifier sets the default uncertainty limit for each analytical datum. In this example a fractional uncertainty limit of 0.025 (2.5 percent) is assumed for all of the analytical data except pH. By default, the uncertainty limit for pH is 0.05 unit. The uncertainty limit for pH can be set to an absolute value (standard units) with -balances identifier. The uncertainty limit for any datum for any of the solutions can be set explicitly to a fractional value or an absolute value (moles; equivalents for alkalinity) using the -balances identifier.
By default, every inverse model includes mole-balance equations for every element in any of the phases included in -phases (except hydrogen and oxygen). If mole-balance equations are needed for elements not included in the phases, that is, for elements with no source or sink (conservative mixing), the -balances identifier can be used to include those elements in the formulation of the inverse-modeling equations (see example 17). In addition, the -balances identifier can be used to specify uncertainty limits for an element in each solution. For demonstration purposes in the example, the uncertainty limit for calcium is set to 0.05 (5 percent) in solution 1 and 0.025 (2.5 percent) in solution 2.
The phases to be used in the inverse-modeling calculations are defined with the -phases identifier. In addition, this identifier can be used to constrain any phases to dissolve only or precipitate only. In this example, kaolinite, Ca-montmorillonite, and chalcedony (SiO 2 ) are required to precipitate only. This means that kaolinite will be precipitating (negative mole transfer) in any model that contains the phase kaolinite; likewise for Ca-montmorillonite and chalcedony. Biotite and plagioclase are required to dissolve (positive mole transfer) if they are present in an inverse model.
All of the phases used in inverse modeling must be defined in PHASES or EXCHANGE_SPECIES data blocks, either in the database file or the input file. Thus, all phases defined in the default database file, phreeqc.dat or wateq4f.dat , are available for use in inverse modeling. Biotite and plagioclase are not in the default database file phreeqc.dat and so they are defined explicitly in the PHASES data block in the input data set. For simplicity, the log K 's are set to zero for these phases, which does not affect inverse modeling because only the mineral stoichiometry is used; however, the saturation indices calculated for these phases will be spurious. All phases used in inverse modeling must have a charge-balanced reaction. This requirement is due to the inclusion of a charge-balance constraint for each solution. Each solution is adjusted to charge balance for each model by adjusting the concentrations of the elements within their uncertainty limits while minimizing the objective function of the optimization method (see "Equations and Numerical Method for Inverse Modeling"). If a solution can not be adjusted to charge balance using the given uncertainty limits, the solution will be noted in the output and no models will be found. Because all of the solutions are charge balanced in the modeling process, phases must also be charge balanced or they will not be included in any models. Note that the reaction for plagioclase (table 48) is on two lines, but the program interprets the two lines to be a single logical line because of the backslash "\" at the end of the first of these two lines.
The -range identifier indicates that, in addition to finding all of the inverse models, each model that is found will be subjected to additional calculations to determine the range of values that each mole transfer may have, within the constraints of the uncertainty limits.
The following equations are included for every inverse model: mole balance for each element or valence state of each element in the system (as defined by elements in the phases of -phases and each element listed in -balances), charge balance for each solution, alkalinity balance for the system, electron balance for the system, and water balance for the system. The unknowns in these equations include the mole transfers of phases, the mole transfers of redox reactions, and the uncertainty unknowns for each element in each solution (excluding hydrogen and oxygen). An uncertainty unknown is included for alkalinity and pH for each solution. The optimization method solves for a set of values for the unknowns that satisfies all of the equations, satisfies all of the uncertainty limits, and simultaneously minimizes the objective function, which is a weighted sum of the uncertainty unknowns (see "Equations and Numerical Method for Inverse Modeling").
Results for the two inverse models found in this example are shown in table 49. The results begin with a listing of three columns for each solution that is part of the model. All columns are values in mol/kgw, except pH (and isotopic values if included). The first column contains the original analytical data for the solution. (Input). The second column contains any adjustments to the analytical data calculated for the model (Delta). These adjustments must be within the specified uncertainty limits. The third column contains the revised analytical data for the solution, which are equal to the original data plus any adjustment (Input+Delta).
After the listing of the solutions, the relative fractions of each solution in the inverse model are printed (Solution fractions). With only two solutions in the model, normally the fraction for each solution will be 1.0. If more than two solutions are included in the inverse model, normally the sum of the fractions of the solutions, excluding the last solution, will equal 1.0. The fractions are actually derived from a mole balance on water, so if hydrated minerals consume or produce significant amounts of water or if evaporation is modeled (see example 17), the numbers may not sum to 1.0. In this example, all fractions are identically 1.0; the amount of water from gypsum dissolution is too small to affect the four significant figures of the mixing fractions. The second and third column for the block giving solution fractions are the minimum and maximum fractional values that can be attained within the constraints of the specified uncertainty limits. These two columns are nonzero only if the -range identifier is used.
The next block of data in the listing contains three columns describing the mole transfers for the phases (Phase mole transfers). The first column contains the inverse model that is consistent with the adjusted concentrations printed in the listing of the solutions. In this example, the adjusted solution 1 plus the mole transfers in the first column exactly equals the adjusted solution 2. Mole transfers that are positive indicate dissolution; mole transfers that are negative indicate precipitation. (Note that mole transfers in phase assemblages in batch-reaction calculations are relative to the phase, not relative to solution.) The second and third columns of mole transfers are the minimum and maximum mole transfers of each phase that can be attained within the constraints of the specified uncertainty limits. These two columns are nonzero only if the -range identifier is used. In general, these minima and maxima are not independent, that is, obtaining a maximum mole transfer of one phase places very strong constraints on the mole transfers of the other phases in a mole-balance model.
No redox mole transfers were calculated in this inverse model. If any redox mole transfers had been calculated, the moles transferred between valence states of each element would be printed under the heading "Redox mole transfers".
The next block of data prints results related to the extent to which the analytical data were adjusted for this model; if no adjustments were made, all three quantities that are printed would be zero. First the sum of residuals is printed, which is a sum of the uncertainty unknowns weighted by the inverse of the uncertainty limit
(
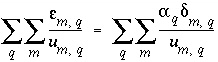). Next, a sum of the adjustment to each element concentration and isotopic com-
position that is weighted by the inverse of the uncertainty limit is printed (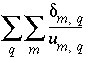
, Sum of delta/uncertainty
limit). Finally, the maximum fractional adjustment to any element or isotopic composition in any solution is printed (Maximum fractional error in element concentration). All three values apply to the model printed in the left-hand column.
For a given mole-balance model, if no simpler inverse model can be found with any proper subset of the solutions and phases of the model, the statement "Model contains minimum number of phases" is printed for the given model.
After all models are printed, a short summary of the calculations is presented, which lists the number of models found, the number of minimal models found (models with a minimum number of phases), the number of infeasible models that were tested, and the number of calls to the inequality equations solver, cl1 (calculation time is generally proportional to the number of calls to cl1).
The results of the example show that two inverse models exist using the phases suggested by Garrels and Mackenzie (1967). The main reactions are dissolution of calcite and plagioclase, which consume carbon dioxide; kaolinite and Ca-montmorillonite precipitate in the first model, and kaolinite and chalcedony precipitate in the second model. Small amounts of halite, gypsum, and biotite dissolution are required in the models. The results of Garrels and Mackenzie (1967) fall within the range of mole transfers calculated in the first model of PHREEQC for all phases except carbon dioxide. The carbon dioxide mole transfer for the first model differs from Garrels and Mackenzie (1967) because they did not account for the dissolved carbon dioxide in the spring waters. Garrels and Mackenzie (1967) also ignored a small discrepancy in the mole balance for potassium. PHREEQC avoids the potassium imbalance by adjusting concentrations of the elements in the two solutions. The PHREEQC calculations show that two inverse models can be found by adjusting concentrations by no more than the specified uncertainty limits (2.5 percent). Without making the calculations with PHREEQC and considering the magnitude of uncertainties, it is not clear whether the discrepancy in potassium that was ignored by Garrels and Mackenzie is significant. The results of PHREEQC are concordant with the results of NETPATH, except that NETPATH also must ignore the discrepancy in the potassium mole balance.
Table 49. --Selected output for example 16
Solution 1:
Input Delta Input+Delta
pH 6.200e+00 + 1.246e-02 = 6.212e+00
Al 0.000e+00 + 0.000e+00 = 0.000e+00
Alkalinity 3.280e-04 + 5.500e-06 = 3.335e-04
C(-4) 0.000e+00 + 0.000e+00 = 0.000e+00
C(4) 7.825e-04 + 0.000e+00 = 7.825e-04
Ca 7.800e-05 + -3.900e-06 = 7.410e-05
Cl 1.400e-05 + 0.000e+00 = 1.400e-05
H(0) 0.000e+00 + 0.000e+00 = 0.000e+00
K 2.800e-05 + -7.000e-07 = 2.730e-05
Mg 2.900e-05 + 0.000e+00 = 2.900e-05
Na 1.340e-04 + 0.000e+00 = 1.340e-04
O(0) 0.000e+00 + 0.000e+00 = 0.000e+00
S(-2) 0.000e+00 + 0.000e+00 = 0.000e+00
S(6) 1.000e-05 + 0.000e+00 = 1.000e-05
Si 2.730e-04 + 0.000e+00 = 2.730e-04
Solution 2:
Input Delta Input+Delta
pH 6.800e+00 + -3.407e-03 = 6.797e+00
Al 0.000e+00 + 0.000e+00 = 0.000e+00
Alkalinity 8.951e-04 + -1.796e-06 = 8.933e-04
C(-4) 0.000e+00 + 0.000e+00 = 0.000e+00
C(4) 1.199e-03 + 0.000e+00 = 1.199e-03
Ca 2.600e-04 + 6.501e-06 = 2.665e-04
Cl 3.000e-05 + 0.000e+00 = 3.000e-05
H(0) 0.000e+00 + 0.000e+00 = 0.000e+00
K 4.000e-05 + 1.000e-06 = 4.100e-05
Mg 7.101e-05 + -8.979e-07 = 7.011e-05
Na 2.590e-04 + 0.000e+00 = 2.590e-04
O(0) 0.000e+00 + 0.000e+00 = 0.000e+00
S(-2) 0.000e+00 + 0.000e+00 = 0.000e+00
S(6) 2.500e-05 + 0.000e+00 = 2.500e-05
Si 4.100e-04 + 0.000e+00 = 4.100e-04
Solution fractions: Minimum Maximum
Solution 1 1.000e+00 1.000e+00 1.000e+00
Solution 2 1.000e+00 1.000e+00 1.000e+00
Phase mole transfers: Minimum Maximum
Halite 1.600e-05 1.490e-05 1.710e-05 NaCl
Gypsum 1.500e-05 1.413e-05 1.588e-05 CaSO4:2H2O
Kaolinite -3.392e-05 -5.587e-05 -1.224e-05 Al2Si2O5(OH)4
Ca-Montmorillon -8.090e-05 -1.100e-04 -5.154e-05 Ca0.165Al2.33Si3.67O10(OH)2
CO2(g) 2.928e-04 2.363e-04 3.563e-04 CO2
Calcite 1.240e-04 1.007e-04 1.309e-04 CaCO3
Biotite 1.370e-05 1.317e-05 1.370e-05 KMg3AlSi3O10(OH)2
Plagioclase 1.758e-04 1.582e-04 1.935e-04 Na0.62Ca0.38Al1.38Si2.62O8
Redox mole transfers:
Sum of residuals (epsilons in documentation): 5.574e+00
Sum of delta/uncertainty limit: 5.574e+00
Maximum fractional error in element concentration: 5.000e-02
Model contains minimum number of phases.
===============================================================================
Solution 1:
Input Delta Input+Delta
pH 6.200e+00 + 1.246e-02 = 6.212e+00
Al 0.000e+00 + 0.000e+00 = 0.000e+00
Alkalinity 3.280e-04 + 5.500e-06 = 3.335e-04
C(-4) 0.000e+00 + 0.000e+00 = 0.000e+00
C(4) 7.825e-04 + 0.000e+00 = 7.825e-04
Ca 7.800e-05 + -3.900e-06 = 7.410e-05
Cl 1.400e-05 + 0.000e+00 = 1.400e-05
H(0) 0.000e+00 + 0.000e+00 = 0.000e+00
K 2.800e-05 + -7.000e-07 = 2.730e-05
Mg 2.900e-05 + 0.000e+00 = 2.900e-05
Na 1.340e-04 + 0.000e+00 = 1.340e-04
O(0) 0.000e+00 + 0.000e+00 = 0.000e+00
S(-2) 0.000e+00 + 0.000e+00 = 0.000e+00
S(6) 1.000e-05 + 0.000e+00 = 1.000e-05
Si 2.730e-04 + 0.000e+00 = 2.730e-04
Solution 2:
Input Delta Input+Delta
pH 6.800e+00 + -3.407e-03 = 6.797e+00
Al 0.000e+00 + 0.000e+00 = 0.000e+00
Alkalinity 8.951e-04 + -1.796e-06 = 8.933e-04
C(-4) 0.000e+00 + 0.000e+00 = 0.000e+00
C(4) 1.199e-03 + 0.000e+00 = 1.199e-03
Ca 2.600e-04 + 6.501e-06 = 2.665e-04
Cl 3.000e-05 + 0.000e+00 = 3.000e-05
H(0) 0.000e+00 + 0.000e+00 = 0.000e+00
K 4.000e-05 + 1.000e-06 = 4.100e-05
Mg 7.101e-05 + -8.980e-07 = 7.011e-05
Na 2.590e-04 + 0.000e+00 = 2.590e-04
O(0) 0.000e+00 + 0.000e+00 = 0.000e+00
S(-2) 0.000e+00 + 0.000e+00 = 0.000e+00
S(6) 2.500e-05 + 0.000e+00 = 2.500e-05
Si 4.100e-04 + 0.000e+00 = 4.100e-04
Solution fractions: Minimum Maximum
Solution 1 1.000e+00 1.000e+00 1.000e+00
Solution 2 1.000e+00 1.000e+00 1.000e+00
Phase mole transfers: Minimum Maximum
Halite 1.600e-05 1.490e-05 1.710e-05 NaCl
Gypsum 1.500e-05 1.413e-05 1.588e-05 CaSO4:2H2O
Kaolinite -1.282e-04 -1.403e-04 -1.159e-04 Al2Si2O5(OH)4
CO2(g) 3.061e-04 2.490e-04 3.703e-04 CO2
Calcite 1.106e-04 8.680e-05 1.182e-04 CaCO3
Chalcedony -1.084e-04 -1.473e-04 -6.906e-05 SiO2
Biotite 1.370e-05 1.317e-05 1.370e-05 KMg3AlSi3O10(OH)2
Plagioclase 1.758e-04 1.582e-04 1.935e-04 Na0.62Ca0.38Al1.38Si2.62O8
Redox mole transfers:
Sum of residuals (epsilons in documentation): 5.574e+00
Sum of delta/uncertainty limit: 5.574e+00
Maximum fractional error in element concentration: 5.000e-02
Model contains minimum number of phases.
===============================================================================
Summary of inverse modeling:
Number of models found: 2
Number of minimal models found: 2
Number of infeasible sets of phases saved: 20
Number of calls to cl1: 62