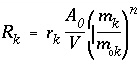 , (94)
, (94)The overall rate for a kinetic reaction of minerals and other solids is:
where r k is the specific rate (mol/m 2 /s), A 0 is the initial surface area of the solid (m 2 ), V is the amount of solution (kgw), m 0 k is the initial moles of solid, m k is the moles of solid at a given time, and ( m k / m 0 k ) n is a factor to account for changes in A 0 / V during dissolution and also for selective dissolution and aging of the solid. For uniformly dissolving spheres and cubes n = 2/3. All calculations in PHREEQC are in moles, and the factor A 0 /V must be provided by the user to obtain the appropriate scaling.
The specific rate expressions,  , for a selection of substances have been included in the database under keyword
RATES. These specific rates have various forms, largely depending on the completeness of the experimental information. When information is lacking, a simple rate that is often applied is
, for a selection of substances have been included in the database under keyword
RATES. These specific rates have various forms, largely depending on the completeness of the experimental information. When information is lacking, a simple rate that is often applied is
where
k
k
is an empirical constant and
IAP
/
K
k
is the saturation ratio (
SR
). This rate equation can be derived from transition-state theory, where the coefficient  is related to the stoichiometry of the reaction when an activated complex is formed (Aagaard and Helgeson, 1982; Delany and others, 1986). Often,
is related to the stoichiometry of the reaction when an activated complex is formed (Aagaard and Helgeson, 1982; Delany and others, 1986). Often,  . An advantage of this expression is that the rate equation applies for both supersaturation and undersaturation, and the rate is zero at equilibrium. The rate is constant over a large domain whenever the geochemical reaction is far from equilibrium (
IAP
/
K
< 0.1), and the rate approaches zero when
IAP
/
K
approaches 1.0 (equilibrium).
. An advantage of this expression is that the rate equation applies for both supersaturation and undersaturation, and the rate is zero at equilibrium. The rate is constant over a large domain whenever the geochemical reaction is far from equilibrium (
IAP
/
K
< 0.1), and the rate approaches zero when
IAP
/
K
approaches 1.0 (equilibrium).
The rate expression may also be based on the saturation index ( SI ) in the following form:
This rate expression has been applied with some success to dissolution of dolomite (Appelo and others, 1984).
Rate expressions often contain concentration-dependent terms. One example is the Monod equation:
where
r
max
is the maximal rate, and
K
m
is equal to the concentration where the rate is half of the maximal rate. The Monod rate equation is commonly used for simulating the sequential steps in the oxidation of organic matter (Van Cappellen and Wang, 1996). A series of rate expressions can be developed in line with the energy yield of the oxidant; first
O
2
is consumed, then 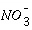 , and successively other, more slowly operating oxidants such as Fe(III) oxides and
, and successively other, more slowly operating oxidants such as Fe(III) oxides and 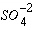 . The coefficients in the Monod equation can be derived from first-order rate equations for the individual processes. For degradation of organic matter (
C
) in soils the first-order rate equation is
. The coefficients in the Monod equation can be derived from first-order rate equations for the individual processes. For degradation of organic matter (
C
) in soils the first-order rate equation is
where
s
C
is organic carbon content (mol/kg soil), and
k
1
is the first-order decay constant (s
-1
). The value of
k
1
is approximately equal to 0.025 yr
-1
in a temperate climate with aerobic soils (Russell, 1973), whereas in sandy aquifers in The Netherlands, where 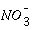 is the oxidant,
is the oxidant, 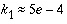 yr
-1
. Concentrations of up to 3
yr
-1
. Concentrations of up to 3 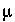 M
O
2
are found in ground water even outside the redox-domain of organic degradation by
O
2
, and 3
M
O
2
are found in ground water even outside the redox-domain of organic degradation by
O
2
, and 3 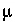 M
O
2
may be taken as the concentration where the (concentration-dependent) rate for aerobic degradation equals the reaction rate for denitrification. First-order decay (
k
1
= 0.025 yr
-1
for 0.3 mM
O
2
and
k
1
= 5e-4 yr
-1
for 3
M
O
2
may be taken as the concentration where the (concentration-dependent) rate for aerobic degradation equals the reaction rate for denitrification. First-order decay (
k
1
= 0.025 yr
-1
for 0.3 mM
O
2
and
k
1
= 5e-4 yr
-1
for 3 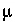 M
O
2
) is obtained with the coefficients
r
max
= 1.57e-9 s
-1
and
K
m
= 294
M
O
2
) is obtained with the coefficients
r
max
= 1.57e-9 s
-1
and
K
m
= 294 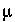 M in the Monod equation, and oxygen as the limiting solute. A similar estimate for denitrification is based on
k
1
= 5e-4 yr
-1
for
M in the Monod equation, and oxygen as the limiting solute. A similar estimate for denitrification is based on
k
1
= 5e-4 yr
-1
for 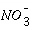 = 3 mM and
k
1
= 1e-5 yr
-1
for
= 3 mM and
k
1
= 1e-5 yr
-1
for 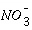 = 3
= 3 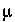 M, which yields
r
max
= 1.67e-11 s
-1
and
K
m
= 155
M, which yields
r
max
= 1.67e-11 s
-1
and
K
m
= 155 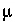 M. The combined overall Monod expression for degradation of organic carbon in a fresh-water aquifer is then:
M. The combined overall Monod expression for degradation of organic carbon in a fresh-water aquifer is then:
where the factor 6 derives from recalculating the concentration of s C from mol/kg soil to mol/kg pore water.
A further aspect of organic matter decomposition is that a part appears to be refractory and particularly
resistant to degradation. Some models have been proposed to account for the tendency of part of the sedimentary organic carbon to survive; tentatively, a factor 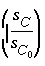 may be assumed, which makes the overall rate second order.
may be assumed, which makes the overall rate second order.
This factor implies that a decrease to 1/10 of the original concentration results in a decrease of 1/100 in the rate of further breakdown. It must be noted that this simple factor is used to approximate a very complicated process and a more thorough treatment of the process is needed, but is also possible given the flexibility of defining rates in PHREEQC.
Still other rate expressions are based on detailed measurements in solutions with varying concentrations of the aqueous species that influence the rate. For example, Williamson and Rimstidt (1994) give a rate expression for oxidation of pyrite:
which shows a square root dependence on the molality of oxygen, and a small increase of the rate with increase in pH. This rate is applicable for the dissolution reaction only, and only when the solution contains oxygen. It is probably inadequate when the solution approaches equilibrium or when oxygen is depleted.
An example of a more complete rate expression which applies for both dissolution and precipitation is the rate equation for calcite. Plummer and others (1978) have found that the rate can be described by the equation:
where bracketed chemical symbols indicate activity, and the coefficients k 1 , k 2 and k 3 have been determined as a function of temperature by Plummer and others (1978) from calcite dissolution experiments in CO 2 -charged solutions. The rate contains a forward part r f (first three terms of equation 101), and a backward part r b (last term of equation 101), and thus is applicable for both dissolution and precipitation. The backward rate contains a coefficient k 4 , the value of which depends on the solution composition. In a pure water-calcite system, bicarbonate concentration is approximately equal to twice the calcium concentration and the backward rate can be approximated as
At equilibrium, 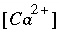 is the activity at saturation
is the activity at saturation 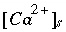 . Also
r
calcite
= 0, and therefore,
. Also
r
calcite
= 0, and therefore,
Combining equations 101, 102, and 103 gives:
In a pure Ca-CO 2 system at constant CO 2 pressure, the ion activity product (IAP) is:
Thus, for a calcite-water system, the rate for calcite can be approximated as:
where r f contains the first three terms given in equation 101.