Table 6.
--Description of Basic program for calcite kinetics given in example for
RATES data block
|
Line
number
|
Function
|
|
1-4
|
Comments.
|
|
10
|
Calculate calcite saturation index.
|
|
20
|
If undersaturated and no moles of calcite, exit; moles=0 by default.
|
|
30-60
|
Calculate temperature dependence of constants k1, k2, and k3.
|
|
70-90
|
Calculate ratio of current moles of calcite to initial moles of calcite, set ratio to 1 if no moles of calcite are present.
|
|
100
|
Calculate surface area.
|
|
110
|
Calculate forward rate.
|
|
130
|
Calculate overall rate, factor of 1e-3 converts rate to moles from millimoles.
|
|
140
|
Calculate moles of reaction over time interval given by TIME. Note that the multiplication of the rate by TIME must be present in one of the Basic lines.
|
|
200
|
Return moles of reaction for time subinterval with "SAVE". A SAVE statement must always be present in a rate program.
|
Table 8.
--Special Basic statements and functions for PHREEQC
|
Special PHREEQC
Statement or Function
|
Explanation
|
|
ACT("HCO3-")
|
Activity of an aqueous, exchange, or surface species.
|
|
ALK
|
Alkalinity of solution.
|
|
CELL_NO
|
Cell number in
TRANSPORT or
ADVECTION calculations
|
|
CHARGE_BALANCE
|
Aqueous charge balance in equivalents.
|
|
DIST
|
Distance to midpoint of cell in
TRANSPORT calculations, cell number in
ADVECTION calculations, "-99" in all other calculations.
|
|
EQUI("Calcite")
|
Moles of a phase in the pure-phase (equilibrium-phase) assemblage.
|
|
EXISTS(
i1
[
, i2, ...
])
|
Determines if a value has been stored with a PUT statement for the list of one or more subscripts.The function equals 1 if a value has been stored and 0 if no value has been stored. Values are stored in global storage with PUT and are accessible by any Basic program. See description of PUT for more details.
|
|
GAS("CO2(g)")
|
Moles of a gas component in the gas phase.
|
|
GET(
i1
[
, i2, ...
])
|
Retrieves the value that is identified by the list of one or more subscripts.Value is zero if PUT has not been used to store a value for the set of subscripts. Values stored in global storage with PUT are accessible by any Basic program. See description of PUT for more details.
|
|
KIN("CH2O")
|
Moles of a kinetic reactant.
|
|
LA("HCO3-")
|
Log10 of activity of an aqueous, exchange, or surface species.
|
|
LM("HCO3-")
|
Log10 of molality of an aqueous, exchange, or surface species.
|
|
M
|
Current moles of reactant for which the rate is being calculated (see
KINETICS).
|
|
M0
|
Initial moles of reactant for which the rate is being calculated (see
KINETICS).
|
|
MISC1("Ca(x)Sr(1-x)SO4")
|
Mole fraction of component 2 at the beginning of the miscibility gap, returns 1.0 if there is no miscibility gap (see
SOLID_SOLUTIONS).
|
|
MISC2("Ca(x)Sr(1-x)SO4")
|
Mole fraction of component 2 at the end of the miscibility gap, returns 1.0 if there is no miscibility gap (see
SOLID_SOLUTIONS).
|
|
MOL("HCO3-")
|
Molality of an aqueous, exchange, or surface species.
|
|
MU
|
Ionic strength of the solution.
|
|
PARM(
i
)
|
Parameter array defined in
KINETICS data block.
|
|
PERCENT_ERROR
|
Percent charge-balance error [100(cations-|anions|)/(cations + |anions|)].
|
|
PRINT
|
Write to output file.
|
|
PUNCH
|
Write to selected-output file.
|
|
PUT(
x
,
i1
[
, i2, ...
])
|
Saves value of
x
in global storage that is identified by a sequence of one or more subscripts. Value of
x
can be retrieved with GET(
i1,
[
, i2, ...
]) and a set of subscripts can be tested to determine if a value has been stored with EXISTS(
i1
[
, i2, ...
]). PUT may be used in
RATES,
USER_PRINT, or
USER_PUNCH Basic programs to store a value. The value may be retrieved by any of these Basic programs. The value persists until overwritten using a PUT statement with the same set of subscripts, or until the end of the run. For a
KINETICS data block, the Basic programs for the rate expressions are evaluated in the order in which they are defined in the input file.
|
|
RXN
|
Amount of reaction (moles) as defined in
-steps in
REACTION data block for a batch-reaction calculation, otherwise zero.
|
|
SAVE
|
Last statement of Basic program that returns the moles of kinetic reactant, counted positive when the solution concentration of the reactant increases.
|
|
SI("Calcite")
|
Saturation index of a phase,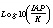 .
.
|
|
SIM_NO
|
Simulation number, equals one more than the number of
END statements before current simulation.
|
|
SIM_TIME
|
Time (s) from the beginning of a kinetic batch-reaction or transport calculation.
|
|
SR("Calcite")
|
Saturation ratio of a phase,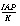 .
.
|
|
STEP_NO
|
Step number in batch-reaction calculations, or shift number in
ADVECTION and
TRANSPORT calculations.
|
|
S_S("MgCO3")
|
Current moles of a solid-solution component.
|
|
TC
|
Temperature in Celsius.
|
|
TK
|
Temperature in Kelvin.
|
|
TIME
|
Time interval for which moles of reaction are calculated in rate programs, automatically set in the time-step algorithm of the numerical integration method.
|
|
TOT("Fe(2)")
|
Total molality of element or element redox state. TOT("water") is total mass of water (kg).
|
|
TOTAL_TIME
|
Cumulative time (s) including all advective (for which
-time_step is defined) and advective-dispersive transport simulations from the beginning of the run or from last
-initial_time identifier.
|
Table 9.
--Standard Basic statements and functions
[Character variables in Basic have "$" as the final character of the variable name]
|
Basic Statements and
Functions
|
Explanation
|
|
+, -, *, /
|
Add, subtract, multiply, and divide.
|
|
string1 + string2
|
String concatenation
|
|
a
^
b
|
Exponentiation, 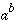 .
.
|
|
<, >, <=, >=, <>, =,
AND, OR, XOR, NOT
|
Relational and Boolean operators.
|
|
ABS(
a
)
|
Absolute value.
|
|
ARCTAN(
a
)
|
Arctangent function.
|
|
ASC(
character
)
|
Ascii value for
character.
|
|
CHR$(
number
)
|
Convert Ascii value to character.
|
|
COS(
a
)
|
Cosine function.
|
|
DIM
a
(
n
)
|
Dimension an array
|
|
DATA
list
|
List of data.
|
|
EXP(
a
)
|
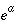 .
.
|
|
FOR
i
=
n
TO
m
STEP
k
NEXT
i
|
"For" loop.
|
|
GOTO
line
|
Go to line number.
|
|
GOSUB
line
|
Go to subroutine.
|
|
IF (
expr
) THEN
statement
ELSE
statement
|
If, then, else statement (on one line; a `\' may be used to concatenate lines).
|
|
LEN(
string
)
|
Number of characters in
string.
|
|
LOG(
a
)
|
Natural logarithm.
|
|
LOG10(
a
)
|
Base 10 logarithm.
|
|
MID$(
string, n
)
MID$(
string, n, m
)
|
Extract characters from position
n
to end of
string.
Extract
m
characters from
string
starting at position
n
.
|
|
a
MOD
b
|
Returns remainder
a
/
b
.
|
|
ON
expr
GOTO
line1
,
line2
, ...
ON
expr
GOSUB
line1
,
line2
, ...
|
If the expression's value, rounded to an integer, is
N
, go to the
N
th line number in the list. If
N
is less than one or greater than the number of line numbers listed, execution continues at the next statement after the ON statement.
|
|
READ
|
Read from DATA statement.
|
|
REM
|
At beginning of line, line is a remark with no effect on the calculations.
|
|
RESTORE
line
|
Set pointer to DATA statement of
line
for subsequent READ.
|
|
RETURN
|
Return from subroutine.
|
|
SGN(
a
)
|
Sign of
a
, +1 or -1.
|
|
SIN(
a
)
|
Sine function.
|
|
SQR(
a
)
|
a
2
.
|
|
SQRT(
a
)
|
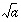 .
.
|
|
STR$(
a
)
|
Convert number to a string.
|
|
TAN(
a
)
|
Tangent function.
|
|
VAL(
string
)
|
Convert string to number.
|
|
WHILE (
expression
)
WEND
|
"While" loop.
|
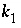 ,
, 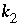 , and
, and 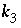 are functions of temperature (Plummer and others, 1978). In a pure calcite-water system with fixed
are functions of temperature (Plummer and others, 1978). In a pure calcite-water system with fixed 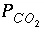 , the overall rate for calcite (forward rate minus backward rate) is approximated by
, the overall rate for calcite (forward rate minus backward rate) is approximated by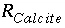 is mmol cm
-2
s
-1
. Equation 156 is implemented in Basic for the first example above. Explanations of the Basic lines for this rate expression are given in table 6.
is mmol cm
-2
s
-1
. Equation 156 is implemented in Basic for the first example above. Explanations of the Basic lines for this rate expression are given in table 6.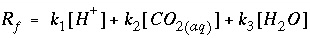 , (155)
, (155)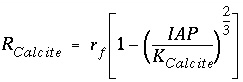 , (156)
, (156)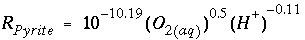 (157)
(157)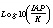 .
.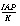 .
.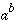 .
.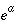 .
.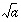 .
.