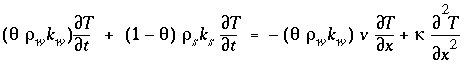 , (117)
, (117)Conservation of heat yields the transport equation for heat, or rather, for the change of temperature. The equation is identical to the advection-reaction-dispersion equation for a chemical substance:
where
T
is the temperature (°C), 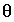 is the porosity (a fraction of total volume, unitless),
is the porosity (a fraction of total volume, unitless), 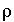 is the density (kg/m
3
),
k
is the specific heat (kJ°C
-1
kg
-1
),
is the density (kg/m
3
),
k
is the specific heat (kJ°C
-1
kg
-1
), 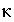 is a term which entails both the dispersion by advective flow and the heat conductivity of the aquifer (kJ°C
-1
m
-1
s
-1
), and subscripts
w
and
s
indicate water and solid, respectively. The temperature
T
is assumed to be uniform over the volume of water and solid.
is a term which entails both the dispersion by advective flow and the heat conductivity of the aquifer (kJ°C
-1
m
-1
s
-1
), and subscripts
w
and
s
indicate water and solid, respectively. The temperature
T
is assumed to be uniform over the volume of water and solid.
Dividing equation 117 by 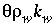 gives:
gives:
where 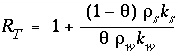 is the temperature retardation factor (unitless), and
is the temperature retardation factor (unitless), and 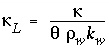 is the thermal dispersion coefficient. The thermal dispersion coefficient contains a component for pure diffusion, and a component for dispersion due to advection:
is the thermal dispersion coefficient. The thermal dispersion coefficient contains a component for pure diffusion, and a component for dispersion due to advection: 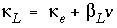 , similar to the hydrodynamic dispersion coefficient. The analogy permits the use of the same numerical scheme for both mass and heat transport.
, similar to the hydrodynamic dispersion coefficient. The analogy permits the use of the same numerical scheme for both mass and heat transport.
De Marsily (1986) suggests that the thermal dispersivity 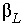 and the hydrodynamic dispersivity
and the hydrodynamic dispersivity 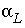 may be equal, whereas the thermal diffusion coefficient
may be equal, whereas the thermal diffusion coefficient 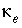 is orders of magnitude larger than
D
e
. Thus, dispersion due to advection can be calculated in the same algorithm for both mass and heat, while thermal diffusion may require an additional calculation when it exceeds hydrodynamic diffusion. When temperatures are different in the column, and when the thermal diffusion coefficient is larger than the hydrodynamic diffusion coefficient, PHREEQC first calculates, for one time step, the temperature distribution and the chemical reactions due to thermal diffusion in excess of the hydrodynamic diffusion. Subsequently PHREEQC calculates transport for the combination of heat and mass due to hydrodynamic diffusion for the time step. The temperature retardation factor and the thermal diffusion coefficient must be defined in the input file (identifier
-thermal_diffusion in keyword
TRANSPORT). Both parameters may vary in time, but are uniform (and temperature independent) over the flow domain.
is orders of magnitude larger than
D
e
. Thus, dispersion due to advection can be calculated in the same algorithm for both mass and heat, while thermal diffusion may require an additional calculation when it exceeds hydrodynamic diffusion. When temperatures are different in the column, and when the thermal diffusion coefficient is larger than the hydrodynamic diffusion coefficient, PHREEQC first calculates, for one time step, the temperature distribution and the chemical reactions due to thermal diffusion in excess of the hydrodynamic diffusion. Subsequently PHREEQC calculates transport for the combination of heat and mass due to hydrodynamic diffusion for the time step. The temperature retardation factor and the thermal diffusion coefficient must be defined in the input file (identifier
-thermal_diffusion in keyword
TRANSPORT). Both parameters may vary in time, but are uniform (and temperature independent) over the flow domain.
The similarity between thermal and hydrodynamic transport is an approximation which mainly falls short because diffusion of mass is by orders of magnitude larger in water than in minerals, whereas diffusion of heat is comparable in the two media although often anisotropic in minerals. The (small) difference in thermal diffusivity leads to complicated heat transfer at phase boundaries which is not accounted for by PHREEQC. Also, PHREEQC does not consider the convection that may develop in response to temperature gradients.