| Next || Previous || Top |
RATES
This keyword data block is used to define mathematical rate expressions for kinetic reactions. General rate formulas are defined in the
RATES
data block and specific kinetic parameters for batch reaction or transport are defined in the KINETICS data block.
Example data block
Line 0: RATES
Line 1: Calcite
Line 2: -start
Basic: 1 rem M = current number of moles of calcite
Basic: 2 rem M0 = number of moles of calcite initially present
Basic: 3 rem PARM(1) = A/V, cm^2/L
Basic: 4 rem PARM(2) = exponent for M/M0
Basic: 10 si_cc = SI("Calcite")
Basic: 20 if (M <= 0 and si_cc < 0) then goto 200
Basic: 30 k1 = 10^(0.198 - 444.0 / TK )
Basic: 40 k2 = 10^(2.84 - 2177.0 / TK)
Basic: 50 if TC <= 25 then k3 = 10^(-5.86 - 317.0 / TK )
Basic: 60 if TC > 25 then k3 = 10^(-1.1 - 1737.0 / TK )
Basic: 70 t = 1
Basic: 80 if M0 > 0 then t = M/M0
Basic: 90 if t = 0 then t = 1
Basic: 100 area = PARM(1) * (t)^PARM(2)
Basic: 110 rf = k1*ACT("H+")+k2*ACT("CO2")+k3*ACT("H2O")
Basic: 120 rem 1e-3 converts mmol to mol
Basic: 130 rate = area * 1e-3 * rf * (1 - 10^(2/3*si_cc))
Basic: 140 moles = rate * TIME
Basic: 200 SAVE moles
Line 3: -end
Line 1a: Pyrite
Line 2a: -start
Basic: 1 rem PARM(1) = log10(A/V, 1/dm)
Basic: 2 rem PARM(2) = exp for (M/M0)
Basic: 3 rem PARM(3) = exp for O2
Basic: 4 rem PARM(4) = exp for H+
Basic: 10 if (M <= 0) then goto 200
Basic: 20 if (SI("Pyrite") >= 0) then goto 200
Basic: 30 lograte = -10.19 + PARM(1) + PARM(2)*LOG10(M/M0)
Basic: 40 lograte = lograte + PARM(3)*LM("O2") + PARM(4)*LM("H+")
Basic: 50 moles = (10^lograte) * TIME
Basic: 60 if (moles > M) then moles = M
Basic: 200 SAVE moles
Line 3a: -end
Explanation
Line 0:
RATES
RATES
is the keyword for the data block. No other data are input on the keyword line.
Line 1:
name of rate expression
name of rate expression
--Alphanumeric character string that identifies the rate expression; no spaces are allowed.
Line 2:
-start
-start
--Identifier marks the beginning of a Basic program by which the moles of reaction for a time subinterval are calculated.
Basic:
numbered Basic statement
numbered Basic statement
--A valid Basic language statement that must be numbered. The statements are evaluated in numerical order. The sequence of statements must extrapolate the rate of reaction over the time subinterval given by the internally defined variable TIME. There must be a statement “
SAVE
expression
”, where the value of
expression
is the moles of reaction that are transferred during time subinterval TIME. Statements and functions that are available through the Basic interpreter are listed in the section on the Basic interpreter. Parameters defined in the KINETICS data block also are available through the Basic array PARM.
Line 3:
-end
-end
--Identifier marks the end of a Basic program by which the number of moles of a reaction for a time subinterval is calculated. Note the hyphen is required to avoid a conflict with the keyword
END
.
Notes
A Basic interpreter (David Gillespie, Synaptics, Inc., San Jose, Calif., written commun., 1997) distributed with the Linux operating system (Free Software Foundation, Inc.) is embedded in PHREEQC. The Basic interpreter is used during the integration of the kinetic reactions to evaluate the moles of reaction progress for a time subinterval. A Basic program for each kinetic reaction must be included in the input or database file. Each program must stand alone with its own set of variables and numbered statement lines. There is no conflict in using the same variable names or line numbers in separate rate programs.
It is possible to transfer data among rates with the special Basic statements PUT and GET (see The Basic Interpreter). The programs are used to calculate the instantaneous rate of reaction and extrapolate that rate for a time subinterval given by the variable “TIME” (calcite, line 140; pyrite line 50). TIME is an internally generated and variable time substep, and its value cannot be changed. The total moles of reaction must be returned to the main program with a SAVE command (line 200 in each example). Note that moles of reaction are returned, not the rate of the reaction. Moles are counted positive when the solution concentration of the reactant increases.
Table 5. Description of Basic program for calcite kinetics given in example for
RATES
data block.
|
Line number
|
Function
|
|
1-4
|
Comments.
|
|
10
|
Calculate calcite saturation index.
|
|
20
|
If undersaturated and no moles of calcite, exit; moles=0 by default.
|
|
30-60
|
Calculate temperature dependence of constants k1, k2, and k3.
|
|
70-90
|
Calculate ratio of current moles of calcite to initial moles of calcite; set ratio to 1 if no moles of calcite are present.
|
|
100
|
Calculate surface area.
|
|
110
|
Calculate forward rate.
|
|
130
|
Calculate overall rate, factor of 1e-3 converts rate to moles from millimoles.
|
|
140
|
Calculate moles of reaction over time interval given by TIME. Note that the multiplication of the rate by TIME must be present in one of the Basic lines.
|
|
200
|
Return moles of reaction for time subinterval with “SAVE”. A SAVE statement must always be present in a rate program.
|
The first example estimates the rate of calcite dissolution or precipitation on the basis of a rate expression from Plummer and others (1978) (see also equations 101 and 106, Parkhurst and Appelo, 1999). The forward rate is given by
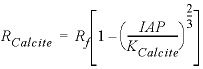 , (2)
, (2)
where 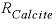 is mmol cm
-2
s
-1
(millimole per square centimeter per second). Equation 2 is implemented in Basic for the first example above. Explanations of the Basic lines for this rate expression are given in table 5.
is mmol cm
-2
s
-1
(millimole per square centimeter per second). Equation 2 is implemented in Basic for the first example above. Explanations of the Basic lines for this rate expression are given in table 5.
The second example is for the dissolution of pyrite in the presence of dissolved oxygen from Williamson and Rimstidt (1994):
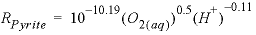 , (3)
, (3)
where parentheses indicate molality. This rate is based on detailed measurements in solutions of varying compositions and shows a square root dependence on the molality of oxygen and a small dependence on pH. This rate is applicable only for dissolution in the presence of oxygen and will be incorrect near equilibrium when oxygen is depleted. Explanations of the Basic lines for this rate expression are given in table 6.
Table 6. Description of Basic program for pyrite dissolution kinetics given in example for
RATES
data block.
|
Line number
|
Function
|
|
1-4
|
Comments.
|
|
10
|
Checks that pyrite is still available, otherwise exits with value of moles=0 by default.
|
|
20
|
Checks that the solution is undersaturated (the rate is for dissolution only), otherwise exits with value of moles=0.
|
|
30, 40
|
Calculate log of the rate of pyrite dissolution.
|
|
50
|
Calculate the moles of pyrite dissolution over time interval given by TIME.
|
|
60
|
Limits pyrite dissolution to remaining moles of pyrite.
|
|
200
|
Return moles of reaction for time subinterval with SAVE. A SAVE statement must always be present in a rate program.
|
Some special statements and functions have been added to the Basic interpreter to allow access to quantities that may be needed in rate expressions. These functions are listed in The Basic Interpreter, table 8. Standard Basic statements that are implemented in the interpreter are listed in The Basic Interpreter, table 7. Upper or lower case may be used for statement, function, and variable names. String variable names must end with the character “$”.
The PRINT command in Basic programs is useful for debugging rate expressions. It can be used to write quantities to the output file to check that rates are calculated correctly. However, the PRINT command will write to the output file every time a rate is evaluated, which may be many times per time step. The sequence of information from PRINT statements in RATES definitions may be difficult to interpret because of the automatic time-step adjustment of the integration method.
Example problems
The keyword
RATES
is used in example problems 6, 9, and 15. It is also found in the Amm.dat, llnl.dat, phreeqc.dat, and wateq4f.dat databases.
| Next || Previous || Top |
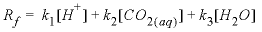 , (1)
, (1)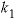 ,
, 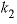 , and
, and 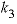 are functions of temperature (Plummer and others, 1978). In a pure calcite-water system with fixed
are functions of temperature (Plummer and others, 1978). In a pure calcite-water system with fixed 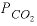 , the overall rate for calcite (forward rate minus backward rate) is approximated by
, the overall rate for calcite (forward rate minus backward rate) is approximated by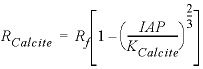 , (2)
, (2) is mmol cm
-2
s
-1
(millimole per square centimeter per second). Equation
is mmol cm
-2
s
-1
(millimole per square centimeter per second). Equation 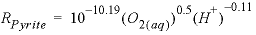 , (3)
, (3)