Explanation
TRANSPORT is the keyword for the data block. No other data are input on the keyword line.
-cells --Indicates the number of cells in the 1D column for the advective-dispersive transport simulation. Optionally, cells or -c [ ells ].
cells --Number of cells in a 1D column. Default is 1.
-shifts --Indicates the number of shifts or diffusion periods in the advective-dispersive transport simulation. Optionally, shifts or -s [ hifts ].
shifts
--For advective-dispersive transport,
shifts
is the number of advective shifts or time steps, which is the number of times the solution in each cell will be shifted to the next higher or lower numbered cell; the total time simulated is 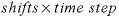 . For purely diffusive transport,
shifts
is the number of diffusion periods that are simulated; the total diffusion time is
. For purely diffusive transport,
shifts
is the number of diffusion periods that are simulated; the total diffusion time is 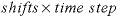 . Default is 1.
. Default is 1.
Line 3: -time_step time_step [unit] [substeps]
-time_step --Defines time step associated with each advective shift or diffusion period. The number of shifts or diffusion periods is given by -shifts . Optionally, timest , -t [ imest ], time_step , or -t [ ime_step ].
time_step --Time (second) associated with each shift or diffusion period. Default is 0 s.
unit --Optional time unit may be second , minute , hour , day , year , or an abbreviation of one of these units. The time_step is converted to seconds after reading the data block; all internal calculations, Basic functions, and output times are in seconds. Default is second.
substeps-- Subdivides the time step into substeps intervals. Used only in multicomponent diffusion calculations, where time_step reduction can help to avoid negative concentrations. The negative concentrations may occur when the time step is too large relative to the explicitly defined stagnant-cell mixing factors; too large a time step causes the Von Neumann criterion to be violated. Default is 1.
Line 4: -flow_direction ( forward , back , or diffusion_only )
-flow_direction --Defines direction of flow. Default is forward at startup. Optionally, direction , flow , flow_direction , -dir [ ection ], or -f [ low_direction ].
forward , back , or diffusion_only --(1) Forward , advective flow direction is into higher numbered cells; optionally, f [ orward ], (2) Backward , advective flow direction is into lower numbered cells; optionally b [ ackward ], or (3) Diffusion_only , only diffusion occurs, there is no advective flow; optionally d [ iffusion_only ] or n [ o_flow ].
Line 5: -boundary_conditions first, last
-boundary_conditions
--Defines boundary conditions for the first and last cell. Optionally,
bc
,
bcond
,
-b
[
cond
],
boundary_condition
,
-b
[
oundary_condition
]. Three types of boundary conditions are allowed at either end of the column (indicated by  ):
):
constant
--Concentration is constant 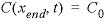 , also known as first type or Dirichlet boundary condition. C
0
is the concentration outside the column (mol/kgw). Optionally,
co
[
nstant
] or
1
.
, also known as first type or Dirichlet boundary condition. C
0
is the concentration outside the column (mol/kgw). Optionally,
co
[
nstant
] or
1
.
closed
--No flux at boundary, v = 0 and 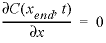 , also known as second type or Neumann boundary condition, where v is the flow velocity (m/s, meter per second). Optionally,
cl
[
osed
] or
2
.
, also known as second type or Neumann boundary condition, where v is the flow velocity (m/s, meter per second). Optionally,
cl
[
osed
] or
2
.
flux
--Flux boundary condition, 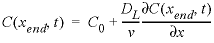 , also known as third type or Cauchy boundary condition, where DL is the dispersion coefficient (m2/s). Optionally,
f
[
lux
] or
3
.
, also known as third type or Cauchy boundary condition, where DL is the dispersion coefficient (m2/s). Optionally,
f
[
lux
] or
3
.
first --Boundary condition at the first cell, constant , closed , or flux . Default is flux .
last --Boundary condition at the last cell, constant , closed , or flux . Default is flux .
Line 6: -lengths list of lengths
-lengths --Defines length of each cell for advective-dispersive transport simulations (m). Optionally, length , lengths , or -l [ engths ].
list of lengths --Length of each cell (m). Any number of lengths up to the total number of cells ( cells ) may be entered. If cells is greater than the number of lengths entered, the final value read will be used for the remaining cells. Multiple lines may be used. Repeat factors can be used to input multiple data with the same value; in the Example data block, 4*1.0 is interpreted as 4 values of 1.0. Default is 1 m.
Line 7: -dispersivities list of dispersivities
-dispersivities --Defines dispersivity of each cell for advective-dispersive transport simulations (m). Optionally, disp , dispersivity , dispersivities , -dis [ persivity ], or -dis [ persivities ].
list of dispersivities --Dispersivity assigned to each cell (m). Any number of dispersivities up to the total number of cells ( cells ) may be entered. If cells is greater than the number of dispersivities entered, the final value read will be used for the remaining cells. Multiple lines may be used. Repeat factors can be used to input multiple data with the same value; in the Example data block, 4*0.1 is interpreted as 4 values of 0.1 m. Default is 0 m.
Line 8: -correct_disp [( True or False )]
-correct_disp --Dispersivity is multiplied by (1 + 1/ cells ) for column ends with flux boundary conditions. This correction can improve modeling effluent composition from column experiments that are modeled with few cells. Default is false at startup. Optionally, correct_disp or -co [ rrect_disp ].
( True or False )-- True indicates that dispersivity is corrected for flux-boundary end cells; false indicates that no correction is made. If neither true nor false is entered on the line, true is assumed. Optionally, t [ rue ] or f [ alse ].
Line 9: -diffusion_coefficient diffusion coefficient
-diffusion_coefficient --Defines diffusion coefficient for all aqueous species (m 2 /s) when not using multicomponent diffusion ( -multi_D false ); this value of the diffusion coefficient is also used as the default thermal diffusion coefficient (see -thermal_diffusion ). Default is 0.3 × 10 -9 m 2 /s at startup. Optionally, diffusion_coefficient , diffc , -dif [ fusion_coefficient ], or -dif [ fc ].
diffusion coefficient --Diffusion coefficient.
Line 10:
-stagnant
stagnant_cells
[
exchange_factor 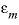
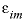 ]
]
-stagnant
--Defines the maximum number of stagnant (immobile) cells associated with each cell in which advection occurs (mobile cell). Each mobile cell may be connected with up to
stagnant_cells
immobile cells. The immobile cells associated with a mobile cell are usually conceived to be a 1D column of cells in which solutes from the mobile cell diffuse laterally. However, the connections among the immobile cells can be defined freely with MIX data blocks, which allows calculation of multidimensional diffusion processes (Appelo and Wersin, 2007) and radial diffusion (Appelo and others, 2008, see See Modeling Diffusion of HTO, 36Cl-, 22Na+, and Cs+ in a Radial Diffusion Cell). The immobile cells associated with a mobile cell,
cell
, are numbered as follows: 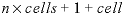 , where
cells
is the number of mobile cells and
, where
cells
is the number of mobile cells and 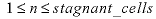 . For each immobile cell, a solution (SOLUTION, SOLUTION_SPREAD, or SAVE data block) must be defined, and either a MIX data block or, for the first-order exchange model, the
exchange_factor
must be defined (only applicable if
stagnant_cells
equals 1). Mixing will be performed at each diffusion/dispersion time step. EQUILIBRIUM_PHASES, EXCHANGE, GAS_PHASE, KINETICS, REACTION, REACTION_TEMPERATURE, SOLID_SOLUTIONS, and SURFACE may be defined for an immobile cell. Thermal diffusion in excess of hydrodynamic diffusion can be calculated only for the first-order exchange model. Optionally,
stagnant
or
-st
[
agnant
].
. For each immobile cell, a solution (SOLUTION, SOLUTION_SPREAD, or SAVE data block) must be defined, and either a MIX data block or, for the first-order exchange model, the
exchange_factor
must be defined (only applicable if
stagnant_cells
equals 1). Mixing will be performed at each diffusion/dispersion time step. EQUILIBRIUM_PHASES, EXCHANGE, GAS_PHASE, KINETICS, REACTION, REACTION_TEMPERATURE, SOLID_SOLUTIONS, and SURFACE may be defined for an immobile cell. Thermal diffusion in excess of hydrodynamic diffusion can be calculated only for the first-order exchange model. Optionally,
stagnant
or
-st
[
agnant
].
stagnant_cells --Maximum number of stagnant (immobile) cells associated with a mobile cell. Default is 0.
exchange_factor --Factor describing exchange between a mobile and its immobile cell (s -1 ). The exchange_factor can be used only if stagnant_cells is 1, in which case all immobile cells have the same diffusion properties. WARNING: If exchange_factor is entered, all previously defined MIX structures will be deleted and MIX structures for the first-order exchange model for a dual porosity medium will be created. Default is 0 s -1 .
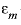 --Porosity in each mobile cell, expressed as a fraction of the total volume of mobile and immobile cells. The
--Porosity in each mobile cell, expressed as a fraction of the total volume of mobile and immobile cells. The
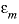 is used only if
stagnant_cells
is 1, in which case all mobile cells have the same porosity. Default is 0 (unitless).
is used only if
stagnant_cells
is 1, in which case all mobile cells have the same porosity. Default is 0 (unitless).
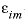 --Porosity in each immobile cell, expressed as a fraction of the total volume of mobile and immobile cells. The
--Porosity in each immobile cell, expressed as a fraction of the total volume of mobile and immobile cells. The
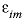 is used only if
stagnant_cells
is 1, in which case all immobile cells have the same porosity. Default is 0 (unitless).
is used only if
stagnant_cells
is 1, in which case all immobile cells have the same porosity. Default is 0 (unitless).
Line 11: -thermal_diffusion temperature retardation factor, thermal diffusion coefficient
-thermal_diffusion
--Defines parameters for calculating the diffusive part of heat transport. Diffusive heat transport will be calculated as a separate process if the temperature in any of the solutions of the transport domain differs by more than 1 °C, and when the
thermal diffusion coefficient
is larger than the effective (aqueous)
diffusion coefficient
. Otherwise, diffusive heat transport is calculated as a part of aqueous diffusion. The
temperature retardation factor
, R
T
, is defined as the ratio of the heat capacity of the total aquifer over the heat capacity of water in the pores, 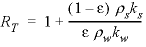 , where
, where 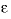 is the water filled porosity,
is the water filled porosity, 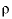 is density (kg/m
3
, kilogram per cubic meter),
k
is specific heat (kJ°C
-1
kg
-1
), and subscripts
w
and
s
indicate water and solid, respectively. The thermal diffusion coefficient,
is density (kg/m
3
, kilogram per cubic meter),
k
is specific heat (kJ°C
-1
kg
-1
), and subscripts
w
and
s
indicate water and solid, respectively. The thermal diffusion coefficient, 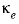 , can be estimated by using
, can be estimated by using 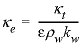 , where
, where 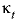 is the heat conductivity of the aquifer, including pore water and solid (kJ°C
-1
m
-1
s
-1
, kilojoule per degree Celsius, per meter per second). The value of
is the heat conductivity of the aquifer, including pore water and solid (kJ°C
-1
m
-1
s
-1
, kilojoule per degree Celsius, per meter per second). The value of 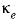 may be 100 to 1500 times larger than the aqueous diffusion coefficient, or about 1
×
10
-6
m
2
/s. A temperature change during transport is reduced by the temperature retardation factor (unitless) to account for the heat capacity of the matrix. Optionally,
-th
[
ermal_diffusion
].
may be 100 to 1500 times larger than the aqueous diffusion coefficient, or about 1
×
10
-6
m
2
/s. A temperature change during transport is reduced by the temperature retardation factor (unitless) to account for the heat capacity of the matrix. Optionally,
-th
[
ermal_diffusion
].
temperature retardation factor --Temperature retardation factor, unitless. Default is 2.0 (unitless).
thermal diffusion coefficient --Thermal diffusion coefficient. Default is the aqueous diffusion coefficient.
Line 12: -initial_time initial_time
-initial_time --Identifier to set the time at the beginning of a transport simulation. The identifier sets the initial value of the variable controlled by -time in the SELECTED_OUTPUT data block. Optionally, initial_time or -i [ nitial_time ].
initial_time --Time (seconds) at the beginning of the transport simulation. Default is the cumulative time including all preceding ADVECTION simulations (for which -time_step has been defined) and all preceding TRANSPORT simulations.
Line 13: -print_cells list of cell numbers
-print_cells --Identifier to select cells for which results will be written to the output file. Optionally, print , print_cells , or -pr [ int_cells ]. Note that the hyphen is required to avoid a conflict with the keyword PRINT.
list of cell numbers --Printing to the output file will occur only for these cell numbers. The list of cell numbers may be continued on the succeeding line(s). A range of cell numbers may be included in the list in the form m-n , where m and n are positive integers, m is less than n , and the two numbers are separated by a hyphen without intervening spaces. Default is 1- cells .
Line 14: -print_frequency print_modulus
-print_frequency --Identifier to select shifts for which results will be written to the output file. Optionally, print_frequency , -print_f [ requency ], output_frequency , or -o [ utput_frequency ].
print_modulus --Printing to the output file will occur for advection shifts or diffusion periods that are evenly divisible by print_modulus . Default is 1.
Line 15: -punch_cells list of cell numbers
-punch_cells --Identifier to select cells for which results will be written to the selected-output file. Optionally, punch , punch_cells , -pu [ nch_cells ], selected_cells , or -selected_c [ ells ].
list of cell numbers --Printing to the selected-output file will occur only for these cell numbers. The list of cell numbers may be continued on the succeeding line(s). A range of cell numbers may be included in the list in the form m-n , where m and n are positive integers, m is less than n , and the two numbers are separated by a hyphen without intervening spaces. Default is 1- cells .
Line 16: -punch_frequency punch_modulus
-punch_frequency --Identifier to select shifts for which results will be written to the selected-output file. Optionally, punch_frequency , -punch_f [ requency ], selected_output_frequency , -selected_o [ utput_frequency ].
punch_modulus --Printing to the selected-output file will occur for advection shifts or diffusion periods that are evenly divisible by punch_modulus . Default is 1.
-dump --Identifier to write a complete state of the advective-dispersive transport simulation to dump file after every dump_modulus advection shifts or diffusion periods. The file is formatted as an input file that can be used to restart calculations. Previous contents of the file are overwritten each time the file is written. Optionally, dump or -du [ mp ].
dump file --Name of the file to which complete state of the advective-dispersive transport simulation will be written. Default is phreeqc.dmp .
Line 18: -dump_frequency dump_modulus
-dump_frequency --Complete state of the advective-dispersive transport simulation will be written to the dump file for advection shifts or diffusion periods that are evenly divisible by dump_modulus . Optionally, dump_frequency or -dump_f [ requency ].
dump_modulus -- Number of advection shifts or diffusion periods. Default is shifts /2 or 1, whichever is larger.
Line 19: -dump_restart shift number
-dump_restart --If an advective-dispersive transport simulation is restarted from a dump file, the starting shift number is given on this line. Optionally, dump_restart or -dump_r [ estart ].
shift number --Starting shift number for the calculations, if restarting from a dump file. The shift number is written in the dump file by PHREEQC. It equals the shift number at which the dump file was created. Default is 1.
Line 20: -warnings [( True or False )]
-warnings --Identifier enables or disables printing of warning messages for transport calculations. In some cases, transport calculations could produce many warnings, which are not errors. Once it is determined that the warnings are not due to erroneous input, disabling the warning messages can avoid generating large output files. Default is true at startup. Optionally, warnings , warning , or -w [ arnings ].
( True or False )--If true , warning messages are printed to the screen and the output file; if false , warning messages are not printed to the screen nor the output file. The value set with -warnings is retained in all subsequent transport simulations until changed. If neither true nor false is entered on the line, true is assumed. Optionally, t [ rue ] or f [ alse ].
Line 21: -multi_D ( True or False ) default_Dw porosity porosity_limit Archie_n
-multi_D --Enables or disables the calculation of multicomponent diffusion. In multicomponent diffusion each solute can be given its own diffusion coefficient, allowing it to diffuse at its own rate, but with the constraint that overall charge balance is maintained (Vinograd and McBain, 1941; Appelo and Wersin, 2007), Optionally, multi_D or -m [ ulti_D ] (as with all identifiers, case insensitive). With -multi_D true , the diffusive flux is calculated by (see also Notes):
where
i
indicates the species;
Ji is the flux (mol m
-2
s
-1
,
mole per square meter per second); 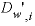 is the (temperature corrected) tracer diffusion coefficient (m
2
/s); ε
is the water-filled (or accessible) porosity (unitless);
n
is an empirical exponent, known from Archie’s law to be about 1;
γ
i
is the activity-coefficient (unitless);
ci
is the concentration (mol/m
3
, mole per cubic meter); grad(
ci
) is the concentration gradient (mol/m
4
, mole per meter to the fourth power)
,
which may be different in free (uncharged) pore water and in the Donnan pore space on a surface (see Notes); and
CBti
is the charge balance term (Appelo and Wersin, 2007, see the Notes).
The tracer diffusion coefficients are defined with keyword
SOLUTION_SPECIES
in
phreeqc.dat
for 25 °C, and corrected to temperature T (K) of the solution as follows:
is the (temperature corrected) tracer diffusion coefficient (m
2
/s); ε
is the water-filled (or accessible) porosity (unitless);
n
is an empirical exponent, known from Archie’s law to be about 1;
γ
i
is the activity-coefficient (unitless);
ci
is the concentration (mol/m
3
, mole per cubic meter); grad(
ci
) is the concentration gradient (mol/m
4
, mole per meter to the fourth power)
,
which may be different in free (uncharged) pore water and in the Donnan pore space on a surface (see Notes); and
CBti
is the charge balance term (Appelo and Wersin, 2007, see the Notes).
The tracer diffusion coefficients are defined with keyword
SOLUTION_SPECIES
in
phreeqc.dat
for 25 °C, and corrected to temperature T (K) of the solution as follows:
where η is the viscosity of water.
When -multi_D is false , the diffusive flux is calculated with J i = - D p × grad( c i ), where D p is the same for all species (defined with identifier -diffusion_coefficient as in Line 9) and not corrected for changes of temperature.
Note that PHREEQC assumes that, for diffusion, the cell contains water exclusively, and uses the pore water diffusion coefficient for calculating the flux. (The effective diffusion coefficient (D e ) is for a volume of grains and pores together, and is related to D p as follows: D e = D p ε ). The identifier -stagnant allows for nonuniform porosities, nonuniform tortuosities, and other variations in the diffusion domain, provided mixing factors among cells are defined explicitly in the input file with MIX data blocks.
( True or False )--If true , multicomponent diffusion is calculated; if false , diffusion is calculated with the diffusion coefficient given in Line 9 .
default_Dw --The diffusion coefficient (m 2 /s at 25 °C) given to solute species for which -dw is not defined in keyword SOLUTION_SPECIES . T he value must be used when calculating explicit mixing factors for stagnant cells. Default is 0 m 2 /s.
porosity --The porosity filled with free and Donnan pore water in the cells; the porosity is a fraction of a representative volume of the porous medium (unitless). Initially all cells are defined with the same porosity . The porosity for a cell can be changed in any keyword data block that supports Basic programming (RATES, USER_GRAPH, USER_PRINT, and USER_PUNCH) by using the PHREEQC Basic function CHANGE_POR(porosity, cell_no). The porosity in a cell can be retrieved with the function GET_POR(cell_no). Default is 0 (unitless).
porosity_limit --The porosity limit, below which diffusion stops. Default is 0 (unitless).
Archie_n
--The exponent n used for calculating the pore-water diffusion coefficient (D
p, i
) from the tracer diffusion coefficient (D
w, i
), Dp, i = Dw, i
ε
n, where
ε
is the water filled (or the accessible) porosity (unitless), and n is an empirical exponent that varies from approximately 0.9 to 1.2 (Grathwohl, 1998; Van Loon and others, 2007) but may be higher for diffusion perpendicular to the bedding plane. The parameter 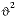 (approximately 1 /
ε
wn) is the tortuosity factor, which accounts for the longer diffusion path for a particle in a porous media than in pure water.
(approximately 1 /
ε
wn) is the tortuosity factor, which accounts for the longer diffusion path for a particle in a porous media than in pure water.
Line 22: -interlayer_D ( True or False ) interlayer_porosity interlayer_porosity_limit interlayer_tortuosity_factor
-interlayer_D
--Enables or disables the calculation of interlayer diffusion in swelling clay minerals. If
-interlayer_D
is
true
,
-multi_D
also must be
true
, and the
-multi_D
parameters must be set as explained with Line 21. Optionally,
interlayer_D
or
-int
[
erlayer_D
] (as with all identifiers, case insensitive). The flux in the interlayers is calculated for the cations associated with X- (as defined with keyword EXCHANGE):
Ji = -
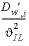 ×
mCEC
×
grad(
βι
) + CBti,
×
mCEC
×
grad(
βι
) + CBti,
where, i indicates an aqueous species, Ji
is the flux (mol m
-2
s
-1
), Dw',i is the temperature corrected diffusion coefficient,
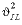 is the interlayer tortuosity factor (unitless), mCEC is the concentration of total X-, mol(X-) / (m3 interlayer water), where (m3 interlayer water) = (m3 free pore water + m3 Donnan water)
×
(
εIL
/
ε
), grad(
βι
) is the gradient of the equivalent fraction of species i on the exchange sites (1/m), and CBti is the charge balance term (Appelo and Wersin, 2007). The tracer diffusion coefficients are defined with keyword
SOLUTION_SPECIES
in
phreeqc.dat
for 25 °C and are corrected to temperature
T
(K) of the solution with the equation
Dw' =
(Dw
)298
×
is the interlayer tortuosity factor (unitless), mCEC is the concentration of total X-, mol(X-) / (m3 interlayer water), where (m3 interlayer water) = (m3 free pore water + m3 Donnan water)
×
(
εIL
/
ε
), grad(
βι
) is the gradient of the equivalent fraction of species i on the exchange sites (1/m), and CBti is the charge balance term (Appelo and Wersin, 2007). The tracer diffusion coefficients are defined with keyword
SOLUTION_SPECIES
in
phreeqc.dat
for 25 °C and are corrected to temperature
T
(K) of the solution with the equation
Dw' =
(Dw
)298
× 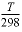 ×
× 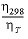 , where
η
is the viscosity of water.
, where
η
is the viscosity of water.
( True or False )--If true , interlayer diffusion is calculated; if false , interlayer diffusion is not calculated .
interlayer_porosity --The porosity of interlayer water, a fraction of the total volume . Default is 0 (unitless) .
interlayer_porosity_limit --The porosity of interlayer water, below which interlayer diffusion stops. Default is 0 (unitless).
interlayer_tortuosity_factor
--The tortuosity factor for interlayer diffusion,
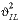 (unitless). Default is 100.0.
(unitless). Default is 100.0.
Line 23: -porosities list of porosities
-porosities--Defines porosity of each cell for diffusive transport simulations (m). Optionally, po[rosities] or -po[rosity].
list of porosities--Porosity of each cell (unitless). Any number of porosities up to the total number of cells (cells) may be entered. If cells is greater than the number of lengths entered, the final value read will be used for the remaining cells. Multiple lines may be used. Repeat factors can be used to input multiple data with the same value; in the Example data block, 4*0.30 is interpreted as 4 values of 0.30. The values entered here take pecedence ofver the value given with -multi_D. If one stangant layer is defined together with an exchange-factor > 0 (‘-stagnant 1 4e-6 0.3 0.1’), the mobile (here = 0.3) and immobile (here = 0.1) porosities defined with -stagnant are used. If -interlayer_d is defined, then the total porosity for a cell is the sum of the porosity defined here and the porosity defined by -interlayer_d.
-fix_current--Current in a column experiment. Default is 0 at startup. Optionally, fix_current, -fi[x_current], or current, or -cu[rrent].
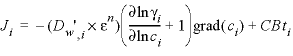 ,
,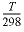 ×
× 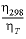 ,
,
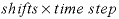 ). The total length of the column is 6 m (four 1-m cells and one 2-m cell).
). The total length of the column is 6 m (four 1-m cells and one 2-m cell). 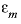 and
and 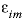 for the mobile and immobile cells.
for the mobile and immobile cells.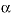 (see equation 125 in Parkhurst and Appelo, 1999).
(see equation 125 in Parkhurst and Appelo, 1999).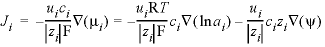 , (10)
, (10)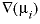 is the gradient of the chemical potential (J mol-1m-1, joule per mole per meter), and similarly for the gradients of lnai and ψ. If the electrical current is zero,
is the gradient of the chemical potential (J mol-1m-1, joule per mole per meter), and similarly for the gradients of lnai and ψ. If the electrical current is zero, 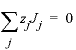 ,
, 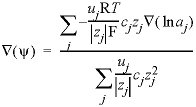 , (11)
, (11)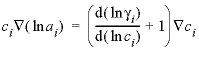 . (12)
. (12)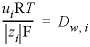 , (13)
, (13)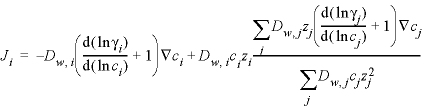 . (14)
. (14)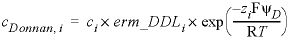 , (15)
, (15)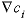 in
in 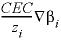 .
.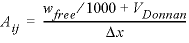 , (17)
, (17)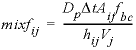 , (18)
, (18)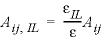 , (19)
, (19)