Evaporation is handled in the same manner as other heterogeneous reactions for inverse modeling. To model evaporation (or dilution), it is necessary to include a phase with the composition “H 2 O”. The important concept in modeling evaporation is the water mole-balance equation (see Parkhurst and Appelo, 1999, “Equations and Numerical Method for Inverse Modeling”). The moles of water in the initial solutions times their mixing fractions, plus water gained or lost by dissolution or precipitation of phases, plus water gained or lost through redox reactions, must equal the moles of water in the final solution. The equation is still approximate because it does not include the moles of water gained or lost in hydrolysis and complexation reactions in the solutions. The results of inverse modeling are compared with a forward model using Pitzer equations to calculate the sequence of salts that precipitate during evaporation.
This example uses data for the evaporation of Black Sea water that is presented in Carpenter (1978). Two analyses are selected, the initial Black Sea water and an evaporated water from which halite has precipitated. The hypothesis is that evaporation, precipitation of calcite, gypsum, and halite, and loss of carbon dioxide are sufficient to account for the changes in water composition of all of the major ions and bromide. The input file (table 49) contains the solution compositions in the SOLUTION data blocks. The total carbon in the solutions is unknown but is estimated by assuming that both solutions are in equilibrium with atmospheric carbon dioxide.
The INVERSE_MODELING keyword defines the inverse model for this example. Solution 2, the solution during halite precipitation, evolves from solution 1, Black Sea water. Uncertainty limits of 2.5 percent are applied to all data. Water, calcite, carbon dioxide, gypsum, and halite are specified to be the potential reactants ( -phases ) that must precipitate, that is, must be removed from the aqueous phase.
Mole-balance equations for water, alkalinity, and electrons are always included in the inverse formulation. In addition, mole-balance equations are included for all the elements in the specified phases, in this case, for calcium, carbon, sulfur, sodium, and chloride. The -balances identifier is used to specify additional mole-balance equations for bromide, magnesium, and potassium. In the absence of alkalinity data, the calculated alkalinity of the solutions is controlled by the pH and the assumption that the solutions are in equilibrium with atmospheric carbon dioxide. Here, alkalinity is a minor contributor to charge balance.
Only one model is found in the inverse calculation. This model indicates that Black Sea water (solution 1) must be concentrated 88-fold to produce solution 2, as shown by the fractions of the two solutions in the inverse-model output (table 50). Thus, approximately 88 kg of water in Black Sea water is reduced to 1 kg of water in solution 2. Halite precipitates (19.75 mol) and gypsum precipitates (0.48 mol) during the evaporation process. Note that these mole transfers are relative to 88 kg of water. To find the loss per kilogram water in Black Sea water, it is necessary to divide by the mixing fraction of solution 1. The result is that 54.9 mol of water, 0.0004 mol of calcite, 0.0004 mol carbon dioxide, 0.0054 mol of gypsum, and 0.22 mol of halite have been removed per kilogram of Black Sea water. (This calculation could be accomplished by making solution 1 from solution 2, taking care to reverse the constraints on minerals from precipitation to dissolution.) All the other ions--magnesium, potassium, and bromide--are conservative within the 2.5-percent uncertainty limit that was specified. The inverse modeling shows that, with the given uncertainty limits, evaporation (loss of water), carbon dioxide outgassing, and calcite, halite, and gypsum precipitation can explain all of the changes in major ion composition.
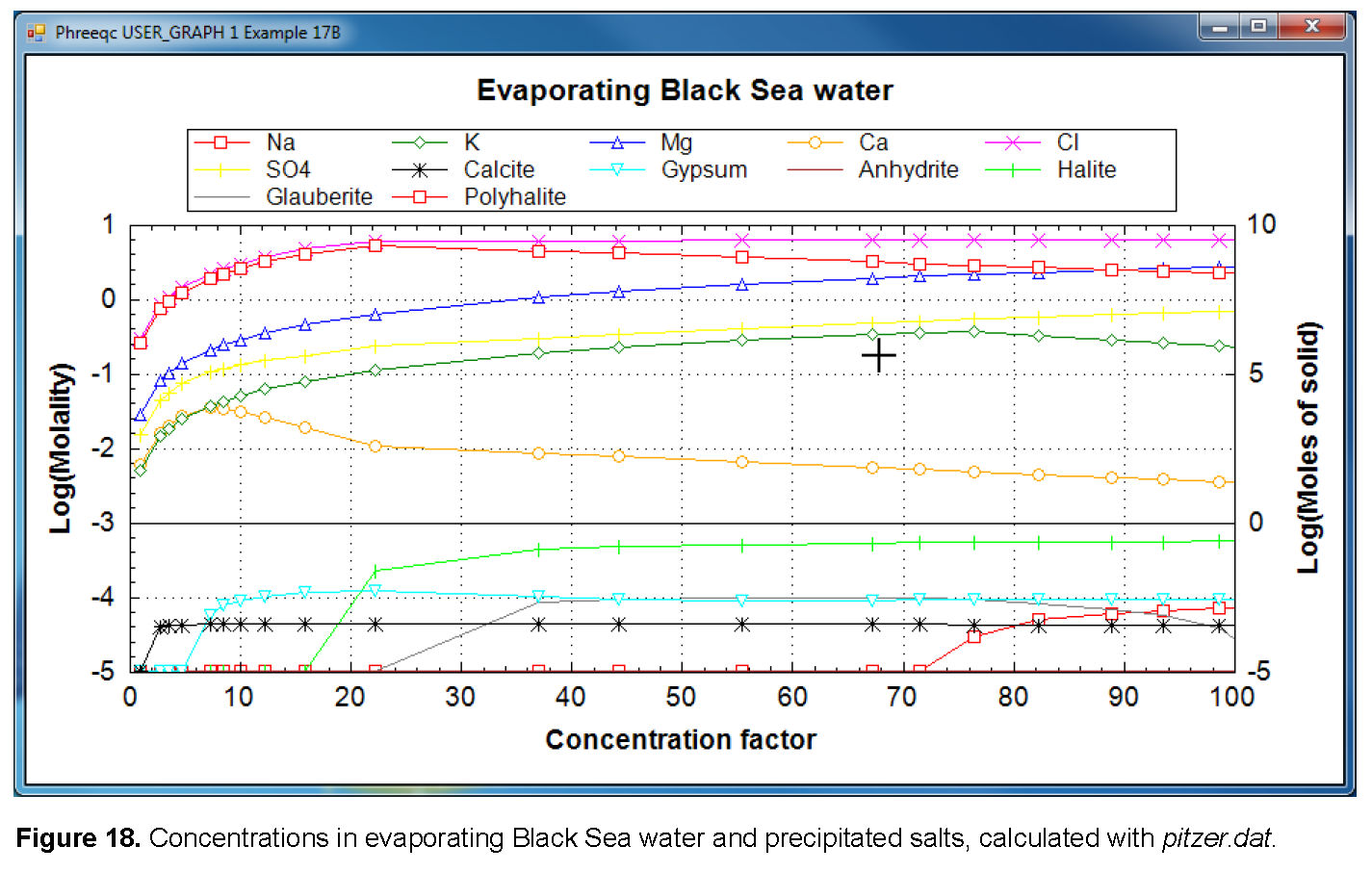
The inverse model can be compared with a forward model that calculates the sequence of salts in evaporating seawater using Pitzer’s equations for solute activities at high ionic strength (Hardie, 1991). The input file is in table 51. The input file allows precipitation (and possibly redissolution) of 12 phases, including carbonates, sulfates, and chlorides. At any point in the evaporation, if the number of moles of a precipitate is less than 1×10 -5 , the number of moles is plotted as 1×10 -5 by USER_GRAPH.
Results of the forward model at 90-fold concentration (fig. 18) show the same mineral precipitates that were included in the inverse model--calcite, gypsum, and halite. However, in the forward model, gypsum precipitates at lower concentration factors, but then transforms to anhydrite slightly before halite starts to precipitate. Similarly, glauberite [Na2Ca(SO4)2] is calculated to precipitate when the water is 30 times concentrated, but redissolves at a concentration factor approaching 90. Polyhalite [K2MgCa2(SO4)4] is calculated to form in the forward model when the water is 80 times concentrated. If glauberite and polyhalite are included in an inverse-modeling calculation (in which solution 2 represents an 88 times concentrated water), neither mineral appears in a mole-balance model. This inverse modeling result for glauberite is consistent with the forward model, which indicates glauberite is redissolved before solution 2 is reached. Polyhalite is not found in the inverse model because precipitation would require the concentration of K+ to decrease (the forward model, with polyhalite precipitation, predicts a K+ concentration of 0.313 M at a concentration factor of 88), whereas the actual concentration in solution 2 (0.46 M) is slightly higher than expected from a concentration factor of 88 and no precipitation reactions (0.005 × 88 = 0.44 M). The inverse model result for polyhalite is consistent with most evaporation experiments, which show that K+ minerals first start to precipitate at somewhat higher concentration factors (McCaffrey and others, 1987; Zherebtsova and Volkova, 1966).
