| Next || Previous || Top |
Example 18--Inverse Modeling of the Madison Aquifer
In this example, inverse modeling, including isotope mole-balance modeling, is applied to the evolution of water in the Madison aquifer in Montana. Plummer and others (1990) used mole-balance modeling to quantify the extent of dedolomitization at locations throughout the aquifer. In the dedolomitization process, anhydrite dissolution causes the precipitation of calcite and dissolution of dolomite. Additional reactions identified by mole-balance modeling include sulfate reduction, cation exchange, and halite and sylvite dissolution (Plummer and others, 1990). 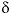 13
C and
13
C and 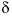 34
S data were used to corroborate the mole-balance models and carbon-14 was used to estimate groundwater ages (Plummer and others, 1990). Initial and final water samples were selected from a flow path that extends from north-central Wyoming northeast across Montana (Plummer and others, 1990, flow path 3). This pair of water samples was selected specifically because it was one of the few pairs that showed a relatively large discrepancy between previous mole-balance approaches and the mole-balance approach of PHREEQC, which includes uncertainties; results for most sample pairs were not significantly different between the two approaches. In addition, this pair of samples was selected because it was modeled in detail in Plummer and others (1990) to determine the sensitivity of mole-balance results to various model assumptions and was used as an example in the netpath manual (Plummer and others, 1994, example 6). Results of PHREEQC calculations are compared to netpath calculations. This example is also discussed in Parkhurst (1997).
34
S data were used to corroborate the mole-balance models and carbon-14 was used to estimate groundwater ages (Plummer and others, 1990). Initial and final water samples were selected from a flow path that extends from north-central Wyoming northeast across Montana (Plummer and others, 1990, flow path 3). This pair of water samples was selected specifically because it was one of the few pairs that showed a relatively large discrepancy between previous mole-balance approaches and the mole-balance approach of PHREEQC, which includes uncertainties; results for most sample pairs were not significantly different between the two approaches. In addition, this pair of samples was selected because it was modeled in detail in Plummer and others (1990) to determine the sensitivity of mole-balance results to various model assumptions and was used as an example in the netpath manual (Plummer and others, 1994, example 6). Results of PHREEQC calculations are compared to netpath calculations. This example is also discussed in Parkhurst (1997).
Water Compositions and Reactants
The initial water for mole-balance modeling (solution 1, table 52) is the recharge water for flow path 3 (Plummer and others, 1990). This calcium-magnesium-bicarbonate water is typical of recharge water in a terrain containing calcite and dolomite. The final water (solution 2, table 52) is a sodium-calcium-sulfate water (with significant chloride concentration) (Plummer and others, 1990, “Mysse Flowing Well”). This water has a charge imbalance of +3.24 meq/kgw (milliequivalent per kilogram water) and contains measurable sulfide. An uncertainty limit of 5 percent was assigned to all chemical data, except iron, for the initial and final waters. The 5-percent uncertainty limit was chosen for the initial water because of spatial uncertainty in the location of a recharge water that is on the same flow path as the final water, and for the final water because it was near the smallest uncertainty limit necessary to obtain charge balance. Iron was assigned an uncertainty limit of 100 percent because of the small concentrations. An uncertainty limit of 0.1 unit was assigned to pH, which is a conservative estimate because of possible CO
2
degassing at this sampling site (L.N. Plummer, U.S. Geological Survey, written commun., 1996). 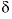 13
C values increase from the initial water to the final water (-7.0 permil to -2.3 permil), as do
13
C values increase from the initial water to the final water (-7.0 permil to -2.3 permil), as do 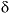 34
S values (9.7 permil to 16.3 permil). Uncertainty limits for isotopic values of the initial solution were set to one-half the range in isotopic composition in four recharge waters from flow paths 3 and 4 (Plummer and others, 1990) (table 52). Similarly, uncertainty limits for isotopic values of the final water were set to one-half the range in isotopic composition in the samples from the distal end of flow path 3 (Plummer and others, 1990) (table 52).
34
S values (9.7 permil to 16.3 permil). Uncertainty limits for isotopic values of the initial solution were set to one-half the range in isotopic composition in four recharge waters from flow paths 3 and 4 (Plummer and others, 1990) (table 52). Similarly, uncertainty limits for isotopic values of the final water were set to one-half the range in isotopic composition in the samples from the distal end of flow path 3 (Plummer and others, 1990) (table 52).
Reactants considered by Plummer and others (1990) were dolomite, calcite, anhydrite, organic matter (CH
2
O), goethite, pyrite, Ca/Na
2
cation exchange, halite, sylvite, and CO
2
gas. In their sensitivity calculations, Mg/Na
2
cation exchange and methane also were considered as potential reactants. The aquifer was considered to be a closed system with respect to CO
2
, that is, no CO
2
is expected to be gained from or lost to a gas phase, and methane gain or loss was considered to be unlikely (Plummer and others, 1990). Therefore, CO
2
gas and methane were not included as reactants in the PHREEQC mole-balance modeling. The uncertainty limits for the isotopic compositions of dissolving phases were taken from data presented in Plummer and others (1990) with slight modifications as follows: 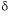 13
C of dolomite, 1 to 5 permil;
13
C of dolomite, 1 to 5 permil; 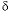 13
C of organic carbon, -30 to -20 permil;
13
C of organic carbon, -30 to -20 permil; 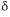 34
S of anhydrite, 11.5 to 15.5 permil. The
34
S of anhydrite, 11.5 to 15.5 permil. The 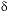 13
C of precipitating calcite depends on the isotopic evolution of the solution and is affected by isotopic fractionation. The fractionation equations are not included in PHREEQC, so it is necessary to assume a compositional range of calcite that represents the average isotopic composition of the precipitating calcite. The average isotopic composition of precipitating calcite from netpath calculations was about -1.5 permil (Plummer and others, 1994) and an uncertainty limit of 1.0 permil was selected to account for uncertainties in fractionation factors. All carbon-14 modeling was done with netpath by using mole transfers from PHREEQC models. The
13
C of precipitating calcite depends on the isotopic evolution of the solution and is affected by isotopic fractionation. The fractionation equations are not included in PHREEQC, so it is necessary to assume a compositional range of calcite that represents the average isotopic composition of the precipitating calcite. The average isotopic composition of precipitating calcite from netpath calculations was about -1.5 permil (Plummer and others, 1994) and an uncertainty limit of 1.0 permil was selected to account for uncertainties in fractionation factors. All carbon-14 modeling was done with netpath by using mole transfers from PHREEQC models. The 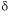 34
S of precipitating pyrite was estimated to be -22 permil (Plummer and others, 1990) with an uncertainty limit of 2 permil; sensitivity analysis indicated that the isotopic value for the precipitating pyrite had little effect on mole transfers. The input file for PHREEQC is shown in table 53. Note that the log
K
values for sylvite, CH
2
O, and the Ca
0.75
Mg
0.25
/Na
2
exchange reaction are set to zero in the
PHASES
and
EXCHANGE_SPECIES
data blocks. The stoichiometry of each of these reactants is correct, which is all that is needed for mole-balance modeling; however, any saturation indices or forward modeling using these reactions would be incorrect because the log
K
values have not been properly defined.
34
S of precipitating pyrite was estimated to be -22 permil (Plummer and others, 1990) with an uncertainty limit of 2 permil; sensitivity analysis indicated that the isotopic value for the precipitating pyrite had little effect on mole transfers. The input file for PHREEQC is shown in table 53. Note that the log
K
values for sylvite, CH
2
O, and the Ca
0.75
Mg
0.25
/Na
2
exchange reaction are set to zero in the
PHASES
and
EXCHANGE_SPECIES
data blocks. The stoichiometry of each of these reactants is correct, which is all that is needed for mole-balance modeling; however, any saturation indices or forward modeling using these reactions would be incorrect because the log
K
values have not been properly defined.
Table 52. Analytical data for solutions used in example 18.
[Charge balance is milliequivalents per kilogram water. All other data are in millimoles per kilogram water, except pH, 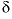 13
C,
13
C, 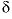 34
S, and
14
C; Fe(2), ferrous iron; TDIC, total dissolved inorganic carbon;
34
S, and
14
C; Fe(2), ferrous iron; TDIC, total dissolved inorganic carbon; 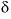 13
C, carbon-13 of TDIC in permil relative to PDB (Pee Dee Belemnite standard);
13
C, carbon-13 of TDIC in permil relative to PDB (Pee Dee Belemnite standard); 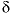 34
S(6), sulfur-34 of sulfate in permil relative to CDT (Canyon Diablo Troilite standard);
34
S(6), sulfur-34 of sulfate in permil relative to CDT (Canyon Diablo Troilite standard); 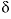 34
S(-2), sulfur-34 of total sulfide in permil relative to CDT;
14
C, carbon-14 in percent modern carbon;
34
S(-2), sulfur-34 of total sulfide in permil relative to CDT;
14
C, carbon-14 in percent modern carbon;  , indicates the uncertainty limit assigned in inverse modeling; --, not measured]
, indicates the uncertainty limit assigned in inverse modeling; --, not measured]
|
Analyte
|
Solution 1
|
Solution 2
|
|
Temperature, °C
|
|
|
|
pH
|
|
|
|
Ca
|
|
|
|
Mg
|
|
|
|
Na
|
|
|
|
K
|
|
|
|
Fe(2)
|
|
|
|
TDIC
|
|
|
|
SO
4
|
|
|
|
H
2
S
|
|
|
|
Cl
|
|
|
|
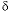 13
C
13
C
|
-
-7.0
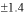 .
.
|
-
-2.3
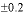
|
|
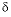 34
S(6)
34
S(6)
|
-
9.7
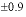
|
-
16.3
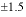
|
|
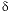 34
S(-2)
34
S(-2)
|
|
-
-22.1
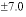
|
|
14
C
|
|
|
|
Charge balance
|
|
|
Table 53. Input file for example 18.
TITLE Example 18.--Inverse modeling of Madison aquifer
|
SOLUTION 1 Recharge number 3
|
units mmol/kgw
|
temp 9.9
|
pe 0.
|
pH 7.55
|
Ca 1.2
|
Mg 1.01
|
Na 0.02
|
K 0.02
|
Fe(2) 0.001
|
Cl 0.02
|
S(6) 0.16
|
S(-2) 0
|
C(4) 4.30
|
-i 13C -7.0 1.4
|
-i 34S 9.7 0.9
|
SOLUTION 2 Mysse
|
units mmol/kgw
|
temp 63.
|
pH 6.61
|
pe 0.
|
redox S(6)/S(-2)
|
Ca 11.28
|
Mg 4.54
|
Na 31.89
|
K 2.54
|
Fe(2) 0.0004
|
Cl 17.85
|
S(6) 19.86
|
S(-2) 0.26
|
C(4) 6.87
|
-i 13C -2.3 0.2
|
-i 34S(6) 16.3 1.5
|
-i 34S(-2) -22.1 7
|
INVERSE_MODELING 1
|
-solutions 1 2
|
-uncertainty 0.05
|
-range
|
-isotopes
|
13C
|
34S
|
-balances
|
Fe(2) 1.0
|
pH 0.1
|
-phases
|
Dolomite dis 13C 3.0 2
|
Calcite pre 13C -1.5 1
|
Anhydrite dis 34S 13.5 2
|
CH2O dis 13C -25.0 5
|
Goethite
|
Pyrite pre 34S -22. 2
|
CaX2 pre
|
Ca.75Mg.25X2 pre
|
MgX2 pre
|
NaX
|
Halite
|
Sylvite
|
PHASES
|
Sylvite
|
KCl = K+ + Cl-
|
-log_k 0.0
|
CH2O
|
CH2O + H2O = CO2 + 4H+ + 4e-
|
-log_k 0.0
|
EXCHANGE_SPECIES
|
0.75Ca+2 + 0.25Mg+2 + 2X- = Ca.75Mg.25X2
|
log_k 0.0
|
END
|
Mole-balance calculations included equations for all elements in the reactive phases (listed under the identifier
-phases
) and for 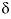 34
S and
34
S and 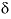 13
C. netpath calculations included isotopic fractionation equations to calculate the
13
C. netpath calculations included isotopic fractionation equations to calculate the 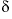 13
C of the final water, thus accounting for fractionation during precipitation, whereas PHREEQC calculated only a mole-balance equation on
13
C of the final water, thus accounting for fractionation during precipitation, whereas PHREEQC calculated only a mole-balance equation on 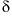 13
C. The adjusted concentrations (original data plus calculated
13
C. The adjusted concentrations (original data plus calculated 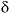 s) from the PHREEQC results were rerun with netpath to obtain carbon-14 ages and to consider the fractionation effects of calcite precipitation. One netpath calculation used the charge-balancing option to identify the effects of charge-balance errors. The charge-balance option of netpath adjusts the concentrations of all cationic elements by a fraction,
s) from the PHREEQC results were rerun with netpath to obtain carbon-14 ages and to consider the fractionation effects of calcite precipitation. One netpath calculation used the charge-balancing option to identify the effects of charge-balance errors. The charge-balance option of netpath adjusts the concentrations of all cationic elements by a fraction, 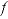 , and of all anionic elements by a fraction
, and of all anionic elements by a fraction 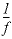 to achieve charge balance for the solution. (The charge-balance option of netpath was improved in version 2.13 to produce exact charge balance; previous versions produced only approximate charge balance.)
to achieve charge balance for the solution. (The charge-balance option of netpath was improved in version 2.13 to produce exact charge balance; previous versions produced only approximate charge balance.)
For all netpath calculations (including the ones that used PHREEQC-adjusted concentrations), carbon dioxide was included as a potentially reactive phase, but the  34
S of anhydrite was adjusted to produce zero mole transfer of carbon dioxide. The
34
S of anhydrite was adjusted to produce zero mole transfer of carbon dioxide. The  13
C of dolomite and organic matter were adjusted within their uncertainty limits to reproduce the
13
C of dolomite and organic matter were adjusted within their uncertainty limits to reproduce the 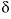 13
C of the final solution as nearly as possible.
13
C of the final solution as nearly as possible.
Madison Aquifer Results and Discussion
The predominant reactions determined by mole-balance modeling are dedolomitization, ion exchange, halite dissolution, and sulfate reduction, as listed in table 54 for the various modeling options discussed next. The driving force for dedolomitization is dissolution of anhydrite (about 20 mmol/kgw, table 54), which causes calcite precipitation and dolomite dissolution. Some of the calcium from anhydrite dissolution and (or) magnesium from dolomite dissolution is taken up by ion-exchange sites, which release sodium to solution. About 15 mmol/kgw of halite dissolves. Sulfate and iron oxyhydroxide reduction by organic matter leads to precipitation of pyrite.
Table 54. Mole-balance results for example 18.
[Results are in millimoles per kilogram water, unless otherwise noted.
14
C, carbon-14 in percent modern carbon (pmc); 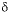 13
C, carbon-13 in permil rPDB (Pee Dee Belemnite);
13
C, carbon-13 in permil rPDB (Pee Dee Belemnite); 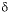 34
S, sulfur-34 in permil CDT (Canyon Diablo Troilite); CH
2
O represents organic matter; Positive numbers for mineral mass transfer indicate dissolution; negative numbers indicate precipitation; For exchange reactions, positive numbers indicate a decrease in calcium and (or) magnesium and an increase in sodium in solution. --, reactant not included in model]
34
S, sulfur-34 in permil CDT (Canyon Diablo Troilite); CH
2
O represents organic matter; Positive numbers for mineral mass transfer indicate dissolution; negative numbers indicate precipitation; For exchange reactions, positive numbers indicate a decrease in calcium and (or) magnesium and an increase in sodium in solution. --, reactant not included in model]
|
Result
|
Ca/Na
2
|
|
Mg/Na
2
|
|
Ca
0.75
Mg
0.25
/Na
|
|
NETPATH
A
|
|
NETPATH
B
|
PHREEQC
B
|
|
NETPATH
C
|
NETPATH
C'
Charge balanced
|
PHREEQC
C
|
|
Ca/Na
2
exchange
|
|
|
|
|
|
|
--
|
--
|
|
Ca
0.75
Mg
0.25
/Na
2
exchange
|
|
|
|
|
|
|
7.6
|
7.7
|
|
Mg/Na
2
exchange
|
|
|
|
|
|
|
--
|
--
|
|
Dolomite [CaMg(CO
3
)
2
]
|
|
|
|
|
|
|
5.3
|
5.4
|
|
Calcite (CaCO
3
)
|
|
|
|
|
|
|
-12.3
|
-12.1
|
|
Anhydrite (CaSO
4
)
|
|
|
|
|
|
|
22.5
|
22.5
|
|
CH
2
O
|
|
|
|
|
|
|
4.3
|
3.5
|
|
Goethite (FeOOH)
|
|
|
|
|
|
|
1.0
|
0.8
|
|
Pyrite (FeS
2
)
|
|
|
|
|
|
|
-1.0
|
-0.8
|
|
Halite (NaCl)
|
|
|
|
|
|
|
15.8
|
15.3
|
|
Sylvite (KCl)
|
|
|
|
|
|
|
2.5
|
2.5
|
|
Carbon dioxide (CO
2
)
|
|
|
|
|
|
|
0.0
|
--
|
|
14
C, reaction adjusted
|
|
|
|
|
|
|
3.8
|
3.8
|
|
Apparent age (year)
|
|
|
|
|
|
|
13,000
|
12,900
|
|
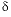 34
S, Anhydrite
34
S, Anhydrite
|
|
|
|
|
|
|
12.5
|
13.4
|
|
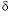 13
C, Dolomite
13
C, Dolomite
|
|
|
|
|
|
|
5.0
|
5.0
|
|
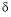 13
C, CH
2
O
13
C, CH
2
O
|
|
|
|
|
|
|
-20.0
|
-20.0
|
|
Calculated 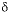 13
C, final water
13
C, final water
|
|
|
|
|
|
|
-4.3
|
-3.3
|
|
Calculated 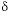 34
S, final water
34
S, final water
|
|
|
|
|
|
|
15.9
|
16.0
|
Plummer and others (1990) realized that the stoichiometry of the exchange reaction was not well defined and considered two variations on these reactions in the sensitivity analysis of the mole-balance model. Pure Ca/Na
2
exchange and pure Mg/Na
2
exchange were considered as potential reactants (netpath
A
and
B
, table 54). When PHREEQC was run with these two reactants, a model was found with Mg/Na
2
(PHREEQC
B
), but no model was found with pure Ca/Na
2
exchange. This difference between netpath and PHREEQC results is attributed to the charge imbalance of the solutions. Solution 2 (table 52) has a charge imbalance of 3.24 meq/kgw, which is more than 3 percent relative to the sum of cation and anion equivalents. This is not a large percentage error, but the absolute magnitude in milliequivalents is large relative to some of the mole transfers of the mole-balance models. When using the revised mole-balance equations in PHREEQC with Ca/Na
2
exchange as the only exchange reaction, it is not possible simultaneously to attain mole balance on elements and isotopes, produce charge balance for each solution, and keep uncertainty terms within the specified uncertainty limits. The exchange reaction with the largest calcium component for which a model could be found was about Ca
0.75
Mg
0.25
/Na
2
(PHREEQC
C
). This exchange reaction was then used in netpath to find netpath
C
. netpath
C'
was calculated by using the charge-balance option of netpath with all phases and constraints the same as in netpath
C
.
One consistent difference between the netpath models without the charge-balance option (netpath
A
,
B
, and
C
) and the PHREEQC models is that the amount of organic-matter oxidation and the mole transfers of goethite and pyrite are larger in the PHREEQC models. These differences are attributed to the effects of charge balance on the mole transfers. It has been noted that charge-balance errors frequently manifest themselves as erroneous mole transfers of single component reactants, such as carbon dioxide or organic matter (Plummer and others, 1994). Except for differences in mole transfers in organic matter, goethite, and pyrite, the Mg/Na
2
models are similar (netpath
B
and PHREEQC
B
). However, both models imply a negative carbon-14 age which is impossible, as noted by Plummer and others (1990).
The PHREEQC model most similar to the pure Ca/Na
2
exchange model (netpath
A
) is the Ca
0.75
Mg
0.25
/Na
2
model (PHREEQC
C
). This model has larger mole transfers of carbonate minerals and organic matter than the Ca/Na
2
model, which decreases the reaction-adjusted carbon-14 activity and produces a younger groundwater age, 12,900 (PHREEQC
C
) compared with 22,700 (netpath
A
). This large change in the calculated age can be attributed to differences in the reactions involving carbon. Two effects can be noted: the change in the exchange reaction and the adjustments for charge-balance errors. The effect of the change in exchange reaction can be estimated from the differences between netpath
A
, which contains pure Ca/Na
2
exchange, and netpath
C
, which contains Ca
0.75
Mg
0.25
/Na
2
exchange, but neither model includes corrections for charge imbalances in the solution compositions. The increase in magnesium in the exchange reaction causes larger mole transfers of calcite and dolomite and decreases the calculated age from 22,700 to 16,500 yr. The effects of charge-balance errors are estimated by the differences between netpath
C
and
C
', which differ only in that the netpath charge-balance option was used in netpath
C
'. Charge balancing the solutions produces larger mole transfers of organic matter and calcite and decreases the calculated age from 16,500 to 13,000 yr. The mole transfers and calculated age for netpath
C
' are similar to PHREEQC
C
but differ slightly because the uncertainty terms in the PHREEQC model have been calculated to achieve not only charge balance but also to reproduce as closely as possible the observed 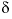 13
C of the final solution.
13
C of the final solution.
One advantage of the revised mole-balance formulation in PHREEQC is that much of the sensitivity analysis that was formerly accomplished by setting up and running multiple models can now be done by including uncertainty limits for all chemical and isotopic data simultaneously. For example, one run of the revised mole-balance formulation determines that no pure Ca/Na
2
model can be found even if any or all of the chemical data were adjusted by as much as plus or minus 10 percent. This kind of information would be difficult and time consuming to establish with previous mole-balance formulations. Another improvement is the explicit inclusion of charge-balance constraints. In this example, including the charge-balance constraint requires a change in the exchange reaction and adjustments to solution composition, which have the combined effect of lowering the estimated maximum age of the groundwater by about 10,000 yr. If Mg/Na
2
exchange is the sole exchange reaction, the age would be modern. Thus, the estimated range in age is large, 0 to 13,000 yr. However, because the calcium to magnesium ratio in solution is approximately 2.5:1 and the cation-exchange constants for calcium and magnesium are approximately equal (Appelo and Postma, 2005), the combined exchange reaction with a dominance for calcium is more plausible, which gives more credence to the older age. Furthermore, comparisons with other carbon-14 ages in the aquifer and with groundwater flow-model ages also indicate that the older end of the age range is more reasonable.
| Next || Previous || Top |
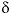 13
C and
13
C and 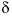 34
S data were used to corroborate the mole-balance models and carbon-14 was used to estimate groundwater ages (Plummer and others, 1990). Initial and final water samples were selected from a flow path that extends from north-central Wyoming northeast across Montana (Plummer and others, 1990, flow path 3). This pair of water samples was selected specifically because it was one of the few pairs that showed a relatively large discrepancy between previous mole-balance approaches and the mole-balance approach of PHREEQC, which includes uncertainties; results for most sample pairs were not significantly different between the two approaches. In addition, this pair of samples was selected because it was modeled in detail in Plummer and others (1990) to determine the sensitivity of mole-balance results to various model assumptions and was used as an example in the netpath manual (Plummer and others, 1994, example 6). Results of PHREEQC calculations are compared to netpath calculations. This example is also discussed in Parkhurst (1997).
34
S data were used to corroborate the mole-balance models and carbon-14 was used to estimate groundwater ages (Plummer and others, 1990). Initial and final water samples were selected from a flow path that extends from north-central Wyoming northeast across Montana (Plummer and others, 1990, flow path 3). This pair of water samples was selected specifically because it was one of the few pairs that showed a relatively large discrepancy between previous mole-balance approaches and the mole-balance approach of PHREEQC, which includes uncertainties; results for most sample pairs were not significantly different between the two approaches. In addition, this pair of samples was selected because it was modeled in detail in Plummer and others (1990) to determine the sensitivity of mole-balance results to various model assumptions and was used as an example in the netpath manual (Plummer and others, 1994, example 6). Results of PHREEQC calculations are compared to netpath calculations. This example is also discussed in Parkhurst (1997).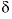 13
C values increase from the initial water to the final water (-7.0 permil to -2.3 permil), as do
13
C values increase from the initial water to the final water (-7.0 permil to -2.3 permil), as do 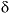 34
S values (9.7 permil to 16.3 permil). Uncertainty limits for isotopic values of the initial solution were set to one-half the range in isotopic composition in four recharge waters from flow paths 3 and 4 (Plummer and others, 1990) (
34
S values (9.7 permil to 16.3 permil). Uncertainty limits for isotopic values of the initial solution were set to one-half the range in isotopic composition in four recharge waters from flow paths 3 and 4 (Plummer and others, 1990) (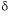 13
C of dolomite, 1 to 5 permil;
13
C of dolomite, 1 to 5 permil; 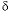 13
C of organic carbon, -30 to -20 permil;
13
C of organic carbon, -30 to -20 permil; 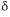 34
S of anhydrite, 11.5 to 15.5 permil. The
34
S of anhydrite, 11.5 to 15.5 permil. The 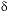 13
C of precipitating calcite depends on the isotopic evolution of the solution and is affected by isotopic fractionation. The fractionation equations are not included in PHREEQC, so it is necessary to assume a compositional range of calcite that represents the average isotopic composition of the precipitating calcite. The average isotopic composition of precipitating calcite from netpath calculations was about -1.5 permil (Plummer and others, 1994) and an uncertainty limit of 1.0 permil was selected to account for uncertainties in fractionation factors. All carbon-14 modeling was done with netpath by using mole transfers from PHREEQC models. The
13
C of precipitating calcite depends on the isotopic evolution of the solution and is affected by isotopic fractionation. The fractionation equations are not included in PHREEQC, so it is necessary to assume a compositional range of calcite that represents the average isotopic composition of the precipitating calcite. The average isotopic composition of precipitating calcite from netpath calculations was about -1.5 permil (Plummer and others, 1994) and an uncertainty limit of 1.0 permil was selected to account for uncertainties in fractionation factors. All carbon-14 modeling was done with netpath by using mole transfers from PHREEQC models. The 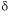 34
S of precipitating pyrite was estimated to be -22 permil (Plummer and others, 1990) with an uncertainty limit of 2 permil; sensitivity analysis indicated that the isotopic value for the precipitating pyrite had little effect on mole transfers. The input file for PHREEQC is shown in
34
S of precipitating pyrite was estimated to be -22 permil (Plummer and others, 1990) with an uncertainty limit of 2 permil; sensitivity analysis indicated that the isotopic value for the precipitating pyrite had little effect on mole transfers. The input file for PHREEQC is shown in 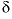 13
C,
13
C, 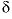 34
S, and
14
C; Fe(2), ferrous iron; TDIC, total dissolved inorganic carbon;
34
S, and
14
C; Fe(2), ferrous iron; TDIC, total dissolved inorganic carbon; 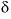 13
C, carbon-13 of TDIC in permil relative to PDB (Pee Dee Belemnite standard);
13
C, carbon-13 of TDIC in permil relative to PDB (Pee Dee Belemnite standard); 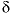 34
S(6), sulfur-34 of sulfate in permil relative to CDT (Canyon Diablo Troilite standard);
34
S(6), sulfur-34 of sulfate in permil relative to CDT (Canyon Diablo Troilite standard); 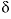 34
S(-2), sulfur-34 of total sulfide in permil relative to CDT;
14
C, carbon-14 in percent modern carbon;
34
S(-2), sulfur-34 of total sulfide in permil relative to CDT;
14
C, carbon-14 in percent modern carbon; 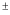 , indicates the uncertainty limit assigned in inverse modeling; --, not measured]
, indicates the uncertainty limit assigned in inverse modeling; --, not measured]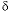 13
C
13
C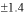 .
.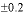
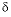 34
S(6)
34
S(6)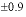
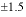
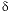 34
S(-2)
34
S(-2)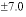
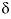 34
S and
34
S and 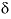 13
C. netpath calculations included isotopic fractionation equations to calculate the
13
C. netpath calculations included isotopic fractionation equations to calculate the 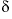 13
C of the final water, thus accounting for fractionation during precipitation, whereas PHREEQC calculated only a mole-balance equation on
13
C of the final water, thus accounting for fractionation during precipitation, whereas PHREEQC calculated only a mole-balance equation on 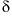 13
C. The adjusted concentrations (original data plus calculated
13
C. The adjusted concentrations (original data plus calculated 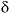 s) from the PHREEQC results were rerun with netpath to obtain carbon-14 ages and to consider the fractionation effects of calcite precipitation. One netpath calculation used the charge-balancing option to identify the effects of charge-balance errors. The charge-balance option of netpath adjusts the concentrations of all cationic elements by a fraction,
s) from the PHREEQC results were rerun with netpath to obtain carbon-14 ages and to consider the fractionation effects of calcite precipitation. One netpath calculation used the charge-balancing option to identify the effects of charge-balance errors. The charge-balance option of netpath adjusts the concentrations of all cationic elements by a fraction, 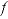 , and of all anionic elements by a fraction
, and of all anionic elements by a fraction 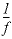 to achieve charge balance for the solution. (The charge-balance option of netpath was improved in version 2.13 to produce exact charge balance; previous versions produced only approximate charge balance.)
to achieve charge balance for the solution. (The charge-balance option of netpath was improved in version 2.13 to produce exact charge balance; previous versions produced only approximate charge balance.)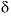 34
S of anhydrite was adjusted to produce zero mole transfer of carbon dioxide. The
34
S of anhydrite was adjusted to produce zero mole transfer of carbon dioxide. The 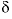 13
C of dolomite and organic matter were adjusted within their uncertainty limits to reproduce the
13
C of dolomite and organic matter were adjusted within their uncertainty limits to reproduce the 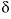 13
C of the final solution as nearly as possible.
13
C of the final solution as nearly as possible.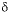 13
C, carbon-13 in permil rPDB (Pee Dee Belemnite);
13
C, carbon-13 in permil rPDB (Pee Dee Belemnite); 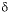 34
S, sulfur-34 in permil CDT (Canyon Diablo Troilite); CH
2
O represents organic matter; Positive numbers for mineral mass transfer indicate dissolution; negative numbers indicate precipitation; For exchange reactions, positive numbers indicate a decrease in calcium and (or) magnesium and an increase in sodium in solution. --, reactant not included in model]
34
S, sulfur-34 in permil CDT (Canyon Diablo Troilite); CH
2
O represents organic matter; Positive numbers for mineral mass transfer indicate dissolution; negative numbers indicate precipitation; For exchange reactions, positive numbers indicate a decrease in calcium and (or) magnesium and an increase in sodium in solution. --, reactant not included in model]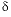 34
S, Anhydrite
34
S, Anhydrite 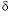 13
C, Dolomite
13
C, Dolomite 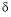 13
C, CH
2
O
13
C, CH
2
O 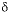 13
C, final water
13
C, final water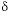 34
S, final water
34
S, final water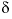 13
C of the final solution.
13
C of the final solution.