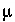mol/kgw KCl solution (
SOLUTION 1-20). Each cell has 48 mmol of exchange sites, which are defined to contain only potassium by the data block
EXCHANGE 1-20. The following example demonstrates the capability of PHREEQC to calculate transient transport of heat and solutes in a column or along a 1D flowline. A column is initially filled with a dilute KCl solution at 25 o C in equilibrium with a cation exchanger. A KNO 3 solution then advects into the column and establishes a new temperature of 0 o C. Subsequently, a sodium chloride solution at 24 o C is allowed to diffuse from both ends of the column, assuming no heat is lost through the column walls. At one end a constant boundary condition is imposed and at the other end the final cell is filled with the sodium chloride solution and a closed boundary condition is prescribed. For the column end with a constant boundary condition, an analytical solution is compared with PHREEQC results, both for retardation R = 1.0 (Cl - ) and R = 3.0 (Na + and temperature). Finally, the second-order accuracy of the numerical method is verified by increasing the number of cells by a factor of three and demonstrating a decrease in the error of the numerical solution by approximately an order of magnitude relative to the analytical solution.
Table 31. --Input data set for example 12
TITLE Example 12.--Advective and diffusive transport of heat and solutes.
Constant boundary condition at one end, closed at other.
The problem is designed so that temperature should equal Na-conc
(in mmol/kgw) after diffusion.
EXCHANGE_SPECIES
Na+ + X- = NaX
log_k 0.0
-gamma 4.0 0.075
H+ + X- = HX
log_k -99.
-gamma 9.0 0.0
K+ + X- = KX
log_k 0.0
-gamma 3.5 0.015
SOLUTION 0 24.0 mM KNO3
units mol/kgw
temp 0 # Incoming solution 0C
pH 7.0
pe 12.0 O2(g) -0.67
K 24.e-3
N(5) 24.e-3
SOLUTION 1-20 0.001 mM KCl
units mol/kgw
temp 25 # Column is at 25C
pH 7.0
pe 12.0 O2(g) -0.67
K 1e-6
Cl 1e-6
EXCHANGE 1-20
KX 0.048
TRANSPORT # Make column temperature 0C, displace Cl
-cells 20
-shifts 19
-flow_d forward
-bcon flux flux
-length 1.0
-disp 0.0 # No dispersion
-diffc 0.0 # No diffusion
-thermal_diffusion 1.0 # No retardation for heat
PRINT
-reset false
END
SOLUTION 0 Fixed temp 24C, and NaCl conc (first type boundary cond) at inlet
units mol/kgw
temp 24
pH 7.0
pe 12.0 O2(g) -0.67
Na 24.e-3
Cl 24.e-3
SOLUTION 20 Same as soln 0 in cell 20 at closed column end (second type boundary cond)
units mol/kgw
temp 24
pH 7.0
pe 12.0 O2(g) -0.67
Na 24.e-3
Cl 24.e-3
EXCHANGE 20
NaX 0.048
TRANSPORT # Diffuse 24C, NaCl solution from column end
-shifts 1
-flow_d diffusion
-bcon constant closed
-thermal_diffusion 3.0 # heat is retarded equal to Na
-diffc 0.3e-9 # m^2/s
-timest 1.0e+10 # 317 years, 19 substeps will be used
SELECTED_OUTPUT
-file ex12.sel
-high_precision true
-reset false
-dist true
-temp true
USER_PUNCH
-head Na_mmol K_mmol Cl_mmol
10 PUNCH TOT("Na")*1000, TOT("K")*1000, TOT("Cl")*1000
END
The input data set for example 12 is shown in table 31. The
EXCHANGE_SPECIES data block is used (1) to make the exchange constant for KX equal to NaX (log_k = 0.0), (2) to effectively remove the possibility of hydrogen ion exchange, and (3) to set activity coefficients for exchange species equal to their aqueous counterparts (
-gamma identifier), so that the exchange between Na
+
and K
+
is linear and the retardation is constant. The infilling solution for transport,
SOLUTION 0, is defined with temperature 0
o
C and 24 mmol/kgw KNO
3
. To stabilize the pe, the concentration of oxygen is defined to be that which is in equilibrium with atmospheric oxygen partial pressure.The column is discretized in 20 cells, which are filled initially with a 1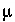
mol/kgw KCl solution (
SOLUTION 1-20). Each cell has 48 mmol of exchange sites, which are defined to contain only potassium by the data block
EXCHANGE 1-20.
The TRANSPORT data block defines cell lengths of 1 m ( -length 1), no dispersion ( -disp 0), no diffusion ( -diffc 0), and no retardation for temperature ( -thermal_diffusion 1). SOLUTION 0 is shifted 19 times into the column ( -shifts 19, -flow_d forward), and arrives in cell 19 at the last shift of the advective-dispersive transport simulation. The boundary conditions at the column ends are of flux type ( -bcon flux flux). In this initial advective-dispersive transport simulation, no exchange occurs (the solution contains only K + as cation, and the exchange sites are completely filled with potassium), and the concentrations and temperatures in the first 19 cells are brought to 24 mmol/kgw KNO 3 and 0 o C. This result could be more easily achieved with SOLUTION data blocks directly (as is done in Attachment C), but the simulation demonstrates how transient boundary and flow conditions can be represented. The dissolved and solid composition and temperature of each cell of the column is automatically saved after each shift in the advective-dispersive transport simulation. The keyword PRINT is used to exclude all printing to the output file ( -reset false).
In the next advective-dispersive transport simulation, diffusion is calculated from the column ends, beginning with the column composition and temperatures that exist following the first advective-dispersive transport calculation, except that a NaCl solution is now defined as solution 0, which diffuses into the top of the column, and as solution 20, which diffuses from the bottom of the column. The new SOLUTION 0 is defined with a temperature of 24 o C and with 24 mmol/kgw NaCl. The last cell ( SOLUTION 20) is also defined to have this solution composition and temperature. The exchanger in cell 20 is defined to be in equilibrium with the new solution composition in cell 20 ( EXCHANGE 20).
The TRANSPORT data block defines one diffusive transport period ( -shifts 1; -flow_d diffusion). The boundary condition at the first cell is constant concentration, and at the last cell the column is closed ( -bcon constant closed). The effective diffusion coefficient ( -diffc) is set to 0.3e-9 m 2 /s, and the time step ( -timest) is defined to be 1.e10 s. Because only one diffusive time period is defined ( -shifts 1), the total time modeled is equal to the time step, 1e10 s. However, the time step will automatically be divided into a number of time substeps to satisfy stability criteria for the numerical method. The heat retardation factor is set to 3.0 ( -thermal_diffusion 3.0). For Na + the ratio of exchangeable concentration (maximum NaX is 48 mmol/kgw) over solute concentration (maximum Na + = 24 mmol/kgw) is 2.0 for all concentrations, and the retardation is therefore R = 1 + d NaX/ d Na + = 3.0, which is numerically equal to the temperature retardation.
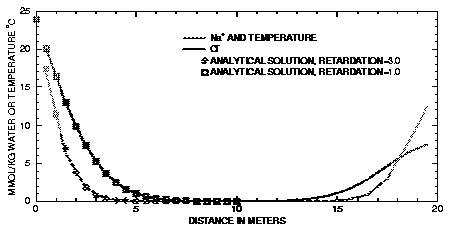
Figure 12. --Simulation results for diffusion from column ends of heat and Na + (retardation R = 3) and Cl - (R = 1) compared with constant-boundary-condition analytical solution.
The SELECTED_OUTPUT data block specifies the name of the selected-output file to be ex12.sel . The identifier " -high_precision true" is used to obtain an increased number of digits in the printing and the identifiers -dist and -temp specify that the distance and temperature of each cell will be printed to the file. The USER_PUNCH data block is used to print concentrations of sodium, potassium, and chloride to the selected-output file in units of mmol/kgw.
In the model, the temperature is calculated with the (linear) retardation formula; however, the Na + concentration is calculated by the cation-exchange reactions. Even though the Na + concentration and the temperature are calculated by different methods, the numerical values should be the same because the initial conditions and the transient conditions are numerically equal and the retardation factors are the same. The temperature and the Na + concentration are equal to at least 6 digits in the PHREEQC selected-output file, which indicates that the algorithm for the chemical transport calculations is correct for the simplified chemistry considered in this example. A further check on the accuracy is obtained by comparing simulation results with an analytical solution. For an infinite column with C x = 0 for t = 0, and diffusion from x = 0 with C x =0 = C 0 for t > 0 the analytical solution is
where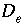 
is the effective diffusion coefficient.
The PHREEQC results are compared with the analytical solution for Cl
-
and for temperature and Na
+
in figure 12 and show excellent agreement. Notice that diffusion of Cl
-
from the column ends has not yet "touched" in the mid-section, so that the column is still effectively infinite and the analytical solution is appropriate. Although both ends of the column started with the same temperature and concentration,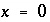 
is maintained at the same temperature and concentrations because of the constant boundary condition. The temperature and concentrations have decreased in cell 20 (plotted at the midpoint of the cell,
x
= 19.5) because of the closed boundary condition that was applied at
x
= 20; no flux of heat or mass through this boundary is allowed and the temperature and concentrations are diminishing because of diffusion into the column. The sodium concentration is not dissipating as rapidly as the chloride concentration because exchange sites must be filled with sodium along the diffusive reach.
Because this example has an analytical solution, it is possible to verify the second-order accuracy of the numerical algorithms used in PHREEQC. For a second-order method, decreasing the cell size by a factor of three should improve the results by about a factor of nine. An input file is given in Attachment C that performs the 20-cell calculation given in this example together with a 60-cell calculation. The deviations from the analytical solution at the end of the time step are calculated at distances from 0.5 to 8.5 m in 0.5 m increments. The results are shown in table 32. As expected for a second-order method, the deviations from the analytical solution decreased by approximately an order of magnitude as the result of decreasing the cell size by a factor of three.
, (160)