Example 13.--
1D Transport in a Dual Porosity Column with Cation Exchange
This example demonstrates the capabilities of PHREEQC to calculate flow in a dual-porosity medium with exchange among the mobile and immobile pores via diffusion. The flexible input format and the modular definition of additional solutions and processes in PHREEQC allow inclusion of heterogeneities and various complexities within a 1D column. This example considers a column filled with small clay beads of 2 cm diameter, which act as stagnant zones. Both the first-order exchange approximation and finite differences are applied in this example, and transport of both a conservative and a retarded (by ion exchange) chemical are considered. It is furthermore shown how a heterogeneous column can be modeled by prescribing mixing factors to account for diffusion between mobile and immobile cells with keyword
MIX.
Stagnant Zone Calculation Using the First-Order Exchange Approximation with Implicit Mixing Factors
The example input file (table 33) is for a column with a uniform distribution of the stagnant porosity along the column. The 20 mobile cells are numbered 1-20. Each mobile cell,
n
, exchanges with one immobile cell, which is numbered 20 + 1 +
n
(cells 22-41 are immobile cells). All cells are given an identical initial solution and exchange complex, but these could be defined differently for each individual cell. It is also possible to distribute the immobile cells over the column non-uniformly, simply by omitting solutions for the stagnant cells that are not present. The connections between the mobile-zone and the stagnant-zone cells and among stagnant zone cells can be varied along the column as well, but this requires that mixing factors among the mobile and immobile cells are prescribed using the keyword
MIX.
As defined in table 33, the column initially contains a 1 mmol/L KNO
3
solution in both the mobile and the stagnant zone (
SOLUTION 1-41). A NaCl-NO
3
solution flows into the column (
SOLUTION 0). An exchange complex with 1 mmol of sites is defined for each cell (
EXCHANGE 1-41), and exchange coefficients are adapted to give linear retardation
R
= 2 for Na
+
(
EXCHANGE_SPECIES). The first
TRANSPORT data block is used to define the physical and flow characteristics of the first transport simulation. The column is 2 m in length and is discretized in 20 cells (
-cells) of 0.1 m (
-length). A pulse of 5 shifts (
-shifts) of the infilling solution (
SOLUTION 0) is introduced into the column. The length of time for each shift is 3600 s (
-timest), which results in a velocity in the mobile pores
v
m
= 0.1 / 3600 = 2.78e-5 m/s. The dispersivity is set to 0.015 m for all cells (
-disp). The diffusion coefficient is set to 0.0 (
-diffc).
The stagnant/mobile interchange is defined using the first-order exchange approximation. The stagnant zone consists of spheres with radius
r
= 0.01 m, diffusion coefficient
D
e
= 3.e-10 m
2
/s, and shape factor 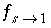 = 0.21 according to table 1 (see "Transport in Dual Porosity Media"). These variables give an exchange factor
= 0.21 according to table 1 (see "Transport in Dual Porosity Media"). These variables give an exchange factor 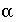 = 6.8e-6 s
-1
. Mobile porosity is
= 6.8e-6 s
-1
. Mobile porosity is 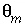 = 0.3 (
-stag) and immobile porosity
= 0.3 (
-stag) and immobile porosity 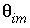 = 0.1. For the first-order exchange approximation in PHREEQC, a single cell immobile zone and the parameters
= 0.1. For the first-order exchange approximation in PHREEQC, a single cell immobile zone and the parameters 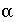 ,
,  and
and 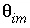 are specified with
-stag. This stagnant zone definition causes each cell in the mobile zone (numbered 1-20) to have an associated cell in the immobile zone (numbered 22-41). The
PRINT data block is used to eliminate all printing to the output file.
are specified with
-stag. This stagnant zone definition causes each cell in the mobile zone (numbered 1-20) to have an associated cell in the immobile zone (numbered 22-41). The
PRINT data block is used to eliminate all printing to the output file.
Following the pulse of NaCl solution, 10 shifts of 1 mmol KNO
3
/L (second
SOLUTION 0) are introduced into the column. The second
TRANSPORT data block does not redefine any of the column or flow characteristics, but specifies that results for cells 1 through 20 (
-punch_cells) be written to the selected output file after 10 shifts (
-punch_frequency). The data blocks
SELECTED_OUTPUT and
USER_PUNCH specify the data to be written to the selected-output file.
Table 33.
--Input data set for example 13A: Stagnant zone with implicitly defined mixing factors
TITLE Example 13A.--1 mmol/l NaCl/NO3 enters column with stagnant zones.
Implicit definition of first-order exchange model.
SOLUTION 0 # 1 mmol/l NaCl
units mmol/l
pH 7.0
pe 13.0 O2(g) -0.7
Na 1.0 # Na has Retardation = 2
Cl 1.0 # Cl has Retardation = 1, stagnant exchange
N(5) 1.0 # NO3 is conservative
# charge imbalance is no problem ...
END
SOLUTION 1-41 # Column with KNO3
units mmol/l
pH 7.0
pe 13.0 O2(g) -0.7
K 1.0
N(5) 1.0
EXCHANGE 1-41
-equil 1
X 1.e-3
EXCHANGE_SPECIES # For linear exchange, make KX exch. coeff. equal to NaX
K+ + X- = KX
log_k 0.0
-gamma 3.5 0.015
END
TRANSPORT
-cells 20
-shifts 5
-flow_d forward
-timest 3600
-bcon flux flux
-diffc 0.0
-length 0.1
-disp 0.015
-stag 1 6.8e-6 0.3 0.1
# 1 stagnant layer^, ^alpha, ^theta(m), ^theta(im)
PRINT
-reset false
END
SOLUTION 0 # Original solution reenters
units mmol/l
pH 7.0
pe 13.0 O2(g) -0.7
K 1.0
N(5) 1.0
TRANSPORT
-shifts 10
-punch_frequency 10
-punch_cells 1-20
SELECTED_OUTPUT
-file ex13a.sel
-reset false
-solution
-distance true
USER_PUNCH
-head Cl_mmol Na_mmol
10 PUNCH TOT("Cl")*1000, TOT("Na")*1000
END
The mixing factors
mixf
m
and
mixf
im
for the first-order exchange approximation for this example are derived from equations 121 and 123 as follows:
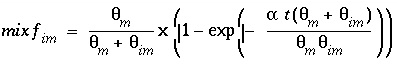 (161)
(161)
and
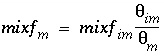 . (162)
. (162)
The retardation factors
R
m
and
R
im
are not included here in the formulas for
mixf
im
and
mixf
m
because in PHREEQC the retardation is a consequence of chemical reactions. According to equations 161 and 162, for this example the mixing factors are calculated to be
mixf
im
= 0.20886 and
mixf
m
= 0.06962. The mixing factors differ for the mobile cell and the immobile cell to account for the difference in the volume of mobile and immobile water.
In PHREEQC, a mixing of mobile and stagnant water is done after each diffusion/dispersion step. This means that the time step decreases when the cells are made smaller and when more diffusive steps ("mixruns") are performed. A 20-cell model as in example 13A has one mixrun. A 100 cell model would have 3 mixruns (equation 110 requires
n
=3 for
mixf
< 1/3), and the time step for calculating
mixf
im
would be (3600/5) / 3 = 240 s. A time step
t
= 240 s leads to
mixf
im
= 0.01614 in the 100 cell model.
Stagnant Zone Calculation Using the First-Order Exchange Approximation with Explicit Mixing Factors
The input file with explicit mixing factors for a uniform distribution of the stagnant zones is given in table 34. The
SOLUTION data blocks are identical to the previous input file. One stagnant layer without further information is defined (
-stag 1, in the
TRANSPORT data block). The mobile/immobile exchange is set by the mix fraction given in the
MIX data blocks. The results of this input file are identical with the results from the previous input file in which the shortcut notation was used. However, the explicit definition of mix factors illustrates that a non-uniform distribution of the stagnant zones, or other physical properties of the stagnant zone, can be included in PHREEQC simulations by varying the mixing fractions which define the exchange among mobile and immobile cells.
Table 34.
--Input data set for example 13B: Stagnant zone with explicitly defined mixing factors
TITLE Example 13B.--1 mmol/l NaCl/NO3 enters column with stagnant zones.
Explicit definition of first-order exchange factors.
SOLUTION 0 # 1 mmol/l NaCl
units mmol/l
pH 7.0
pe 13.0 O2(g) -0.7
Na 1.0 # Na has Retardation = 2
Cl 1.0 # Cl has Retardation = 1, stagnant exchange
N(5) 1.0 # NO3 is conservative
# charge imbalance is no problem ...
END
SOLUTION 1-41 # Column with KNO3
units mmol/l
pH 7.0
pe 13.0 O2(g) -0.7
K 1.0
N(5) 1.0
EXCHANGE 1-41
-equil 1
X 1.e-3
EXCHANGE_SPECIES # For linear exchange, make KX exch. coeff. equal to NaX
K+ + X- = KX
log_k 0.0
-gamma 3.5 0.015
END
MIX 1; 1 .93038; 22 .06962 ;MIX 2; 2 .93038; 23 .06962;
MIX 3; 3 .93038; 24 .06962 ;MIX 4; 4 .93038; 25 .06962;
MIX 5; 5 .93038; 26 .06962 ;MIX 6; 6 .93038; 27 .06962;
MIX 7; 7 .93038; 28 .06962 ;MIX 8; 8 .93038; 29 .06962;
MIX 9; 9 .93038; 30 .06962 ;MIX 10; 10 .93038; 31 .06962;
MIX 11; 11 .93038; 32 .06962 ;MIX 12; 12 .93038; 33 .06962;
MIX 13; 13 .93038; 34 .06962 ;MIX 14; 14 .93038; 35 .06962;
MIX 15; 15 .93038; 36 .06962 ;MIX 16; 16 .93038; 37 .06962;
MIX 17; 17 .93038; 38 .06962 ;MIX 18; 18 .93038; 39 .06962;
MIX 19; 19 .93038; 40 .06962 ;MIX 20; 20 .93038; 41 .06962;
#
MIX 22; 1 .20886; 22 .79114 ;MIX 23; 2 .20886; 23 .79114;
MIX 24; 3 .20886; 24 .79114 ;MIX 25; 4 .20886; 25 .79114;
MIX 26; 5 .20886; 26 .79114 ;MIX 27; 6 .20886; 27 .79114;
MIX 28; 7 .20886; 28 .79114 ;MIX 29; 8 .20886; 29 .79114;
MIX 30; 9 .20886; 30 .79114 ;MIX 31; 10 .20886; 31 .79114;
MIX 32; 11 .20886; 32 .79114 ;MIX 33; 12 .20886; 33 .79114;
MIX 34; 13 .20886; 34 .79114 ;MIX 35; 14 .20886; 35 .79114;
MIX 36; 15 .20886; 36 .79114 ;MIX 37; 16 .20886; 37 .79114;
MIX 38; 17 .20886; 38 .79114 ;MIX 39; 18 .20886; 39 .79114;
MIX 40; 19 .20886; 40 .79114 ;MIX 41; 20 .20886; 41 .79114;
TRANSPORT
-cells 20
-shifts 5
-flow_d forward
-timest 3600
-bcon flux flux
-diffc 0.0
-length 0.1
-disp 0.015
-stag 1
PRINT
-reset false
END
SOLUTION 0 # Original solution reenters
units mmol/l
pH 7.0
pe 13.0 O2(g) -0.7
K 1.0
N(5) 1.0
TRANSPORT
-shifts 10
-punch_frequency 10
-punch_cells 1-20
SELECTED_OUTPUT
-file ex13b.sel
-reset false
-distance true
-solution
USER_PUNCH
-head Cl_mmol Na_mmol
10 PUNCH TOT("Cl")*1000, TOT("Na")*1000
END
Stagnant Zone Calculation Using a Finite Difference Approximation
The stagnant zone consists of spheres with radius
r
= 0.01 m. Diffusion into the spheres induces radially symmetric concentration changes according to the differential equation:
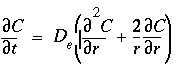 . (163)
. (163)
The calculation in finite differences can therefore be simplified to one (radial) dimension..
Table 35.
--Mixing factors for finite difference calculation of diffusion in spheres
|
Cell
|
r, m
|
V
j,
m
3
|
A
ij,
m
2
|
h
ij,
m
|
f
bc
|
mixf
ij
|
mixf
jj
|
mixf
jk
|
|
102
|
0.001
|
3.35e-8
|
5.03e-5
|
0.002
|
1
|
0.81
|
0.19
|
-
|
|
82
|
.003
|
2.35e-7
|
2.01e-4
|
.002
|
1
|
.463
|
.421
|
0.116
|
|
62
|
.005
|
6.37e-7
|
4.52e-4
|
.002
|
1
|
.384
|
.446
|
.170
|
|
42
|
.007
|
1.24e-6
|
8.04e-4
|
.002
|
1
|
.350
|
.453
|
.197
|
|
22
|
.009
|
2.04e-6
|
1.26e-3
|
.002
|
1.72
|
.571
|
.217
|
.212
|
|
1
|
-
|
1.26e-5
|
-
|
-
|
-
|
-
|
.907
|
.093
|
The calculation follows the theory outlined in the section "Transport in Dual Porosity Media" of this manual. The stagnant zone is divided into a number of layers that mix by diffusion. In this example, the sphere is cut in 5 equidistant layers with 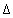 r
= 0.002 m. Five stagnant layers are defined under keyword
TRANSPORT with
-stagnant 5 (table 36). Mixing is specified among adjacent cells in the stagnant layers with
MIX data blocks; the mixing factors are calculated by equations 128 and 129. For the calculation, the volume
V
j
of cell
j
(m
3
) is needed, the shared surface area
A
ij
of cell
i
and
j
(m
2
), the distance between midpoints
h
ij
of cells
i
and
j
(m), and the correction factor for boundary cells
f
bc
(dimensionless). The values for mobile cell 1 and associated immobile cells are given in table 35. The cells in the immobile layer are numbered as
n
+
l
x
cells
+ 1, where
n
is the number of a mobile cell,
l
is the number of the stagnant layer, and
cells
is the total number of mobile cells. In this example, the boundary cell in the stagnant zone for cell number 1 is cell number 22 and the other four stagnant layers are cell numbers 42, 62, 82, and 102, with number 102 being the innermost cell of the sphere, which is connected only to one other cell (cell 82). The volume of the mobile cell (cell 1) is expressed relative to the volume of a sphere of radius 0.01 m, by multiplying this volume with
r
= 0.002 m. Five stagnant layers are defined under keyword
TRANSPORT with
-stagnant 5 (table 36). Mixing is specified among adjacent cells in the stagnant layers with
MIX data blocks; the mixing factors are calculated by equations 128 and 129. For the calculation, the volume
V
j
of cell
j
(m
3
) is needed, the shared surface area
A
ij
of cell
i
and
j
(m
2
), the distance between midpoints
h
ij
of cells
i
and
j
(m), and the correction factor for boundary cells
f
bc
(dimensionless). The values for mobile cell 1 and associated immobile cells are given in table 35. The cells in the immobile layer are numbered as
n
+
l
x
cells
+ 1, where
n
is the number of a mobile cell,
l
is the number of the stagnant layer, and
cells
is the total number of mobile cells. In this example, the boundary cell in the stagnant zone for cell number 1 is cell number 22 and the other four stagnant layers are cell numbers 42, 62, 82, and 102, with number 102 being the innermost cell of the sphere, which is connected only to one other cell (cell 82). The volume of the mobile cell (cell 1) is expressed relative to the volume of a sphere of radius 0.01 m, by multiplying this volume with 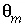 /
/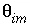 (4.19e-6 ∞ 0.3 / 0.1 = 1.26e-5). In table 35 the value for
f
bc
is 1.72 as calculated from equation 127. It may be noted that using
f
bc
= 1.81 slightly improves the fit to an analytical solution given in Crank (1975) for diffusion into spheres in a closed vessel (a beaker with solution and clay beads). However, changing
f
bc
to 1.81 has little effect on the concentration profiles for the column which are shown in figure 13
(4.19e-6 ∞ 0.3 / 0.1 = 1.26e-5). In table 35 the value for
f
bc
is 1.72 as calculated from equation 127. It may be noted that using
f
bc
= 1.81 slightly improves the fit to an analytical solution given in Crank (1975) for diffusion into spheres in a closed vessel (a beaker with solution and clay beads). However, changing
f
bc
to 1.81 has little effect on the concentration profiles for the column which are shown in figure 13
Table 36.
--Input data set for example 13C: Stagnant zone with diffusion calculated by finite differences (partial listing)
TITLE Example 13C.--1 mmol/l NaCl/NO3 enters column with stagnant zones.
5 layer stagnant zone with finite differences.
SOLUTION 0 # 1 mmol/l NaCl
units mmol/l
pH 7.0
pe 13.0 O2(g) -0.7
Na 1.0 # Na has Retardation = 2
Cl 1.0 # Cl has Retardation = 1, stagnant exchange
N(5) 1.0 # NO3 is conservative
# charge imbalance is no problem ...
END
SOLUTION 1-121 # Column with KNO3
units mmol/l
pH 7.0
pe 13.0 O2(g) -0.7
K 1.0
N(5) 1.0
EXCHANGE 1-121
-equil 1
X 1.e-3
EXCHANGE_SPECIES # For linear exchange, make KX exch. coeff. equal to NaX
K+ + X- = KX
log_k 0.0
-gamma 3.5 0.015
END
MIX 1; 1 0.90712; 22 0.09288
MIX 22; 1 0.57098; 22 0.21656; 42 0.21246
MIX 42; 22 0.35027; 42 0.45270; 62 0.19703
MIX 62; 42 0.38368; 62 0.44579; 82 0.17053
MIX 82; 62 0.46286; 82 0.42143; 102 0.11571
MIX 102; 82 0.81000; 102 0.19000
#
# MIX definitions omitted for mobile cells
# 2-19 and associated immobile cells
#
MIX 20; 20 0.90712; 41 0.09288
MIX 41; 20 0.57098; 41 0.21656; 61 0.21246
MIX 61; 41 0.35027; 61 0.45270; 81 0.19703
MIX 81; 61 0.38368; 81 0.44579; 101 0.17053
MIX 101; 81 0.46286; 101 0.42143; 121 0.11571
MIX 121; 101 0.81000; 121 0.19000
TRANSPORT
-cells 20
-shifts 5
-flow_direction forward
-timest 3600
-tempr 3.0
-bcond flux flux
-diffc 0.0
-length 0.10
-disp 0.015
-stag 5
PRINT
-reset false
END
SOLUTION 0 # Original solution reenters
units mmol/l
pH 7.0
pe 13.0 O2(g) -0.7
K 1.0
N(5) 1.0
TRANSPORT
-shifts 10
-punch_frequency 10
-punch_cells 1-20
SELECTED_OUTPUT
-file ex13c.sel
-reset false
-solution
-distance true
USER_PUNCH
-head Cl_mmol Na_mmol
10 PUNCH TOT("Cl")*1000, TOT("Na")*1000
END
Note in table 36 that 121 solutions are defined, 1-20 for the mobile cells, and the rest for the immobile cells. The input file is identical with the previous one, except for
-stag 5 and the mixing factors among the cells. Not all the mixing factors are shown in table 36, they are identical for subsequent cells and their neighboring stagnant cells. In this example with clay beads, only radial (1D) diffusion is considered, and only mixing among cells in different layers is defined. However, it is possible to include mixing among the immobile cells of adjacent mobile cells.
Figure 13.
--Results of simulations of transport with diffusion into spherical stagnant zones modeled using finite difference and first-order exchange approximations.
Figure 13 compares the concentration profiles in the mobile cells obtained with example 13A (and B) with example 13C. The basic features of the two simulations are the same. The positions of the peaks, as calculated by the two simulations, are similar. The Cl
-
peak is near 1.2 m, but would be at about 1.45 m in the absence of stagnant zones. The integrated concentrations in the mobile porosity are about equal for the first-order exchange and the finite difference simulations. The exchange factor 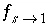 = 0.21 for the first-order exchange approximation appears to provide adequate accuracy for this simulation. However, the first-order exchange approximation produces lower peaks and more tailing than the more exact solution obtained with finite differences. Discrepancies can also appear as deviations in the breakthrough curve (Van Genuchten, 1985). The first-order exchange model is probably least accurate when applied to simulating the transport behavior of spheres; other shapes of the stagnant area can give a better correspondence. It is clear that the linear exchange model is much easier to apply because any explicit model requires the preparation of extended lists of mixing factors (notice that a separate simulation with
USER_PUNCH can serve that purpose), which change when the discretization is adapted. The calculation time for a finite difference model with multiple immobile-zone layers may also be considerably longer than for the single immobile-zone layer of the first-order exchange approximation.
= 0.21 for the first-order exchange approximation appears to provide adequate accuracy for this simulation. However, the first-order exchange approximation produces lower peaks and more tailing than the more exact solution obtained with finite differences. Discrepancies can also appear as deviations in the breakthrough curve (Van Genuchten, 1985). The first-order exchange model is probably least accurate when applied to simulating the transport behavior of spheres; other shapes of the stagnant area can give a better correspondence. It is clear that the linear exchange model is much easier to apply because any explicit model requires the preparation of extended lists of mixing factors (notice that a separate simulation with
USER_PUNCH can serve that purpose), which change when the discretization is adapted. The calculation time for a finite difference model with multiple immobile-zone layers may also be considerably longer than for the single immobile-zone layer of the first-order exchange approximation.
| Next|| Previous || Top |
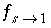 = 0.21 according to table 1 (see "Transport in Dual Porosity Media"). These variables give an exchange factor
= 0.21 according to table 1 (see "Transport in Dual Porosity Media"). These variables give an exchange factor 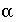 = 6.8e-6 s
-1
. Mobile porosity is
= 6.8e-6 s
-1
. Mobile porosity is 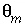 = 0.3 (
-stag) and immobile porosity
= 0.3 (
-stag) and immobile porosity 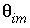 = 0.1. For the first-order exchange approximation in PHREEQC, a single cell immobile zone and the parameters
= 0.1. For the first-order exchange approximation in PHREEQC, a single cell immobile zone and the parameters 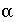 ,
,  and
and 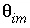 are specified with
-stag. This stagnant zone definition causes each cell in the mobile zone (numbered 1-20) to have an associated cell in the immobile zone (numbered 22-41). The
PRINT data block is used to eliminate all printing to the output file.
are specified with
-stag. This stagnant zone definition causes each cell in the mobile zone (numbered 1-20) to have an associated cell in the immobile zone (numbered 22-41). The
PRINT data block is used to eliminate all printing to the output file.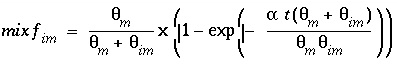 (161)
(161)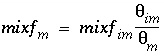 . (162)
. (162)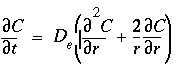 . (163)
. (163)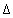 r
= 0.002 m. Five stagnant layers are defined under keyword
r
= 0.002 m. Five stagnant layers are defined under keyword
 /
/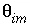 (4.19e-6 ∞ 0.3 / 0.1 = 1.26e-5). In table
(4.19e-6 ∞ 0.3 / 0.1 = 1.26e-5). In table 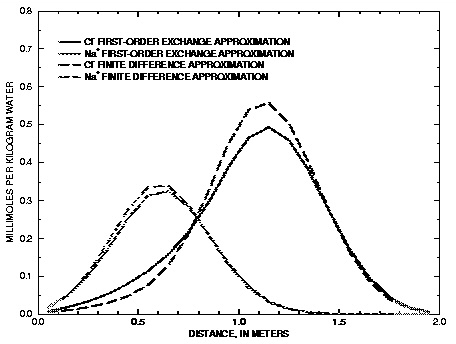
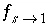 = 0.21 for the first-order exchange approximation appears to provide adequate accuracy for this simulation. However, the first-order exchange approximation produces lower peaks and more tailing than the more exact solution obtained with finite differences. Discrepancies can also appear as deviations in the breakthrough curve (Van Genuchten, 1985). The first-order exchange model is probably least accurate when applied to simulating the transport behavior of spheres; other shapes of the stagnant area can give a better correspondence. It is clear that the linear exchange model is much easier to apply because any explicit model requires the preparation of extended lists of mixing factors (notice that a separate simulation with
= 0.21 for the first-order exchange approximation appears to provide adequate accuracy for this simulation. However, the first-order exchange approximation produces lower peaks and more tailing than the more exact solution obtained with finite differences. Discrepancies can also appear as deviations in the breakthrough curve (Van Genuchten, 1985). The first-order exchange model is probably least accurate when applied to simulating the transport behavior of spheres; other shapes of the stagnant area can give a better correspondence. It is clear that the linear exchange model is much easier to apply because any explicit model requires the preparation of extended lists of mixing factors (notice that a separate simulation with