| Next || Previous || Top |
PHASES
This keyword data block is used to define a name, chemical reaction, log
K
, and temperature dependence of log
K
for each gas component and mineral that can be used for speciation, batch-reaction, transport, or inverse-modeling calculations. In addition, molar volumes can be defined for solids, and the critical temperature and pressure and the acentric factor can be defined for gases. Normally, this data block is included in the database file and only additions and modifications are included in the input file.
Example data block 1
Line 0: PHASES
Line 1a: Gypsum
Line 2a: CaSO4:2H2O = Ca+2 + SO4-2 + 2H2O
Line 3a: log_k -4.58
Line 4a: delta_h -0.109
Line 5: -analytical_expression 68.2401 0.0 -3221.51 -25.0627
Line 6: -Vm 73.9 cm3/mol
Line 1b: O2(g)
Line 2b: O2 = O2
Line 3b: log_k -2.96
Line 4b: delta_h 1.844
Line 7: -T_c 154.6
Line 8: -P_c 49.80
Line 9: -Omega 0.021
Explanation 1
Line 0:
PHASES
Keyword for the data block. No other data are input on the keyword line.
Line 1:
Phase name
phase name
--Alphanumeric name of phase; no spaces are allowed.
Line 2:
Dissolution reaction
Dissolution reaction for phase to aqueous species. Any aqueous species, including e
-
, may be used in the dissolution reaction. The chemical formula for the defined phase must be the first chemical formula on the left-hand side of the equation. The dissolution reaction must precede any identifiers related to the phase. The stoichiometric coefficient for the phase in the chemical reaction must be 1.0.
Line 3:
log_k
log K
log_k
--Identifier for log
K
at 25 °C. Optionally,
-log_k
,
logk
,
-l
[
og_k
], or
-l
[
ogk
].
log K
--Log
K
at 25 °C for the reaction. Default is 0.0.
Line 4:
delta_h
enthalpy,
[
units
]
delta_h
--Identifier for enthalpy of reaction at 25 °C. Optionally,
-delta_h
,
deltah
,
-d
[
elta_h
], or
-d
[
eltah
].
enthalpy
--Enthalpy of reaction at 25 °C for the reaction. Default is 0.0.
units
--Units may be calories, kilocalories, joules, or kilojoules per mole. Only the energy unit is needed (per mole is implied) and abbreviations of these units are acceptable. Explicit definition of units for all enthalpy values is recommended. The enthalpy of reaction is used in the Van’t Hoff equation to determine the temperature dependence of the equilibrium constant. Internally, all enthalpy calculations are performed in the units of kJ/mol. Default units are kJ/mol.
Line 5:
-analytical_expression
A
1
,
A
2
,
A
3
,
A
4
,
A
5
,
A
6
-analytical_expression
--Identifier for coefficients for an analytical expression for the temperature dependence of log
K
. If defined, the analytical expression takes precedence over
log_k
and the Van’t Hoff equation to determine the temperature dependence of the equilibrium constant. Optionally,
analytical_expression
,
a_e
,
ae
,
-a
[
nalytical_expression
],
-a
[
_e
],
-a
[
e
].
A
1
, A
2
, A
3
, A
4
, A
5
,
A
6
--Six values defining log
K
as a function of temperature in the expression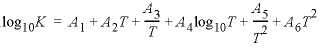 , where
T
is kelvin. Coefficients are defined in order from
A
1
to
A
6
; if less than six parameters are defined, the undefined parameters are set to zero.
, where
T
is kelvin. Coefficients are defined in order from
A
1
to
A
6
; if less than six parameters are defined, the undefined parameters are set to zero.
Line 6:
-Vm
molar_volume [units]
-Vm
--Identifier for the molar volume of the solid phase.
molar_volume
, the molecular weight divided by the density of the solid at 25 °C. In the example for gypsum 172.18 (g/mol, gram per mole) / 2.33 (g/cm
3
, gram per cubic centimeter) = 73.9 cm
3
/mol (cubic centimeter per gram). Default is 0 cm
3
/mol.
units
--Units may be cm
3
/mol, dm
3
/mol (cubic decimeter per mole), or m
3
/mol (cubic meter per mole). Default is cm
3
/mol.
Line 7:
-T_c
critical temperature
-T_c
--Identifier for the critical temperature of the gas.
critical temperature
--Temperature, K (kelvin). Default is 0 K.
Line 8:
-P_c
critical pressure
-P_c
--Identifier for the critical pressure of the gas.
critical pressure
--Pressure, atm. Default is 0 atm.
Line 9:
-Omega
acentric factor
-Omega
--Identifier for the acentric factor of the gas.
acentric factor
--Acentric factor dimensionless. Default is 0.
Notes 1
The set of Lines 1 and 2 must be entered in order, and either Line 3 (
log_k
) or Line 5 (
-analytical_expression
) should be entered for each phase (default log K is 0.0). The analytical expression (
-analytical_expression
) takes precedence over
log_k and
the Van’t Hoff equation (
delta_H
) to determine the temperature dependence of the equilibrium constant. Lines 3 to 5, Line 6 for a solid, and Lines 7 to 9 for a gas may be entered as needed in any order. The equations for the phases may be written in terms of any aqueous chemical species, including e
-
.
The molar volume of a solid is, together with the volumes of the solute species, used to calculate the pressure dependence of
log_k
:
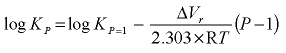 ,
,
where P is pressure (atm),
Δ
V
r
is the volume change of the reaction (cm
3
/mol), R is the gas constant (82.06 atm cm
3
mol
-1
K
-1
, atmosphere cubic centimeter per mole per kelvin), and T is the temperature (K).
The critical temperature and pressure and the acentric factor of a gas are used to calculate the equation of state according to Peng and Robinson (1976):
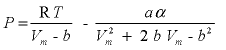 ,
,
where V
m
is the molar volume of the gas (cm
3
/mol), b is the minimal volume of the gas (cm
3
/mol), a is the Van der Waals attraction factor (atm cm
3
mol
-2
, atmosphere cubic centimeter per mole squared) and
α
is a dimensionless function of reduced temperature and acentric factor. With P and Vm known, the fugacity coefficient of a gas can be calculated as:
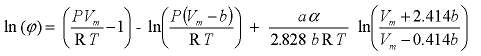 ,
,
where
ϕ
is the fugacity coefficient. The product of the fugacity coefficient and the gas pressure yields the activity of the gas which can be entered in the law of mass action.
For a multicomponent gas phase, the weighted sums are taken of a, b, and α:
b
sum
= Σ(x
i
b), where x
i
is mole-fraction of gas i,
aα
sum
= Σ
i
( Σ
j
(x
i
x
j
(a
i
α
i
a
j
α
j
)
0.5
) ) (1 - k
ij
), and
k
ij
= binary interaction coefficient.
As a result, the fugacity coefficient of a gas in a mixture will be different from the fugacity coefficient of the pure gas at the same pressure.
The identifier
-no_check
can be used to disable checking charge and elemental balances (see SOLUTION_SPECIES). The use of
-no_check
is not recommended, except in cases where the phase is only to be used for inverse modeling. Even in this case, equations defining phases should be charge balanced. The identifier also can be used to define the mineral formula for an exchanger with an explicit charge imbalance (see explanation under EXCHANGE).
Example data block 2
Line 0: PHASES
Line 1: CH3D(g)
Line 2: CH3D(g) + H2O(l) = CH4(g) + HDO(aq)
Line 3: log_k -0.301029995663
Line 4: -add_logk Log_alpha_D_CH4(g)/H2O(l) -1.0
Line 1a: Ca[34S]O4:2H2O
Line 2a: Ca[34S]O4:2H2O + SO4-2 = [34S]O4-2 + Gypsum(s)
Line 4a: -add_logk Log_alpha_34S_Gypsum/SO4-2 -1.0
Line 1b: Gypsum
Line 2b: CaSO4:2H2O = Ca+2 + SO4-2 + 2 H2O
Line 3a: log_k -4.580
Explanation 2
Line 0:
PHASES
Keyword for the data block. No other data are input on the keyword line.
Line 1:
Phase name
phase name
--Alphanumeric name of phase; no spaces are allowed.
Line 2:
Dissolution reaction
Dissolution reaction for phase. In implementing isotope calculations, the dissolution reaction was generalized to allow, in addition to any aqueous species, solid and gas species. To distinguish solids and gases (defined in the PHASES data block) from aqueous species, “(s)” and “(g)” are appended to the species in the equation. For clarity, “H2O(l)” can be used in an equation to designate liquid water, but it is equivalent to using “H2O”. The chemical formula for the defined phase must be the first chemical formula on the left-hand side of the equation. The stoichiometric coefficient for the defined phase in the chemical reaction must be 1.0. The dissolution reaction must precede any identifiers related to the phase.
Line 3:
log_k
log K
log_k
--Identifier for log
K
at 25 °C. Optionally,
-log_k
,
logk
,
-l
[
og_k
], or
-l
[
ogk
].
log K
--Log
K
at 25 °C for the reaction. Default is 0.0.
Line 4:
-add_logk
named_expression, coefficient
-add_logk
--The value of the
named_expression
is multiplied by the
coefficient
and added to the log K for the phase. This identifier may be used multiple times in the definition of the equilibrium constant for the phase. Optionally,
add_logk
,
add_log_k
,
-ad
[
d_logk
] or
-ad
[
d_log_k
].
named_expression
--Name of an expression defined in a NAMED_EXPRESSIONS data block.
coefficient
--The
coefficient
is multiplied by the value of the
named_expression
and added to the equilibrium constant for the phase.
Notes 2
Example data block 2 demonstrates capabilities that were added during the implementation of isotopic calculations as described by Thorstenson and Parkhurst (2000, 2004). First, to simplify the definition of equilibrium constants for the isotopic variants of a mineral or gas, the dissociation reaction was generalized to allow solids and gases in the equation. Solids are identified by an appended “(s)” and gases are identified by an appended “(g)”. The original definition of the solid or gas may or may not have the appended string in its name; PHREEQC attempts to find the name in the list of phases with and without the appended string. Note in this example that “Gypsum(s)” is used in Line 2a, but “Gypsum” is defined as the name of the phase in Line 1b.
When specifying individual equilibrium constants for isotopic phases, a single fractionation factor may appear in the expressions of the equilibrium constants for multiple isotopic forms of a phase. To avoid many manipulations with analytical expressions in the definition of equilibrium constants, the NAMED_EXPRESSIONS data block allows assigning a name to the expression for a fractionation factor. This named expression can then be used in calculating the equilibrium constants for phases defined in the
PHASES
data block by use of the
-add_logk
identifier. In the definition of CH3D(g) in the Example data block 2, the fractionation factor for deuterium between methane and liquid water is added to an equilibrium constant derived from the symmetry of the molecule to define the equilibrium constant for the dissociation reaction.
Example problems
The keyword
PHASES
is used in example problems 1, 6, 7, 8, 9, 10, 16, 18, and 21. It is also found in all of the database files.
| Next || Previous || Top |
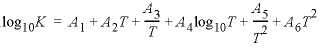 , where
T
is kelvin. Coefficients are defined in order from
A
1
to
A
6
; if less than six parameters are defined, the undefined parameters are set to zero.
, where
T
is kelvin. Coefficients are defined in order from
A
1
to
A
6
; if less than six parameters are defined, the undefined parameters are set to zero. 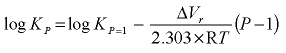 ,
, 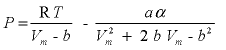 ,
,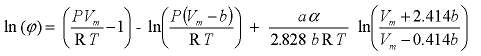 ,
,