Flow Over 2D & 3D Dunes
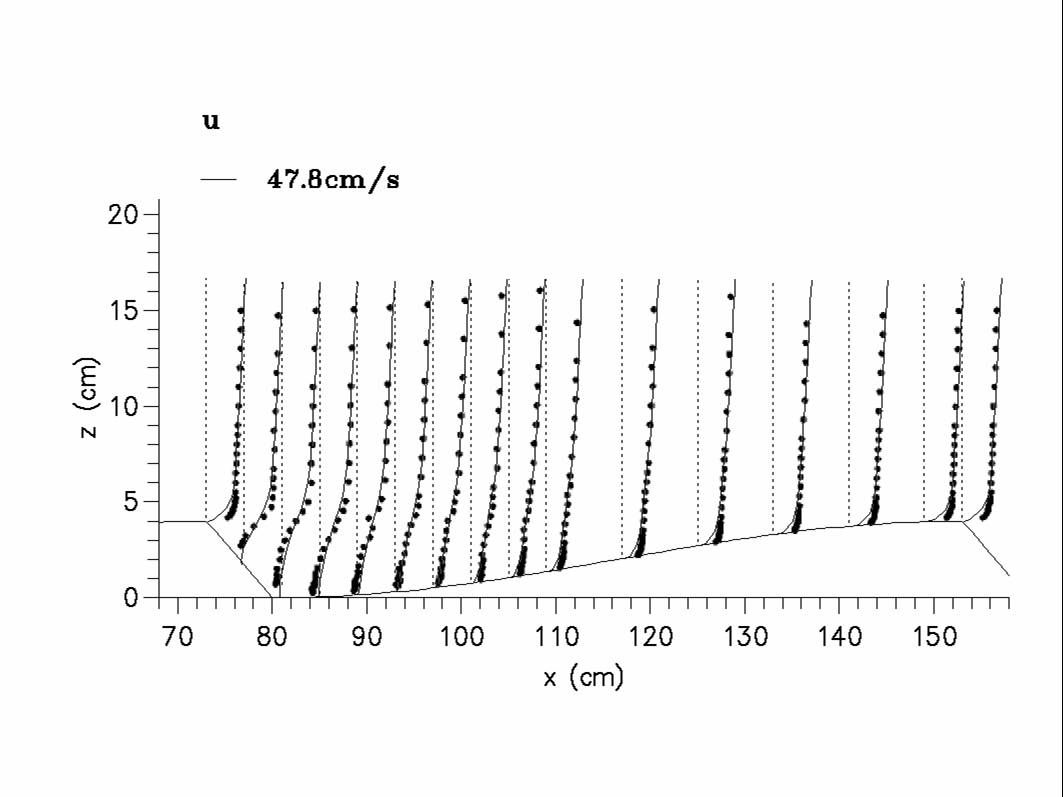
As part of a program aimed at extending current computational morphodynamics capabilities to include two- and three-dimensional bedforms, we tested two computational codes for computing flow over bedforms, both developed by Yasuyuki Shimizu and his colleagues at the University of Hokkaido. First, we used a direct numerical simulation (DNS) model with and without sub-grid scale closures to compute the flow over two- and three-dimensional bedforms for which laboratory data sets of velocity and pressure are available. As shown in the following figures, this approach works well for predicting mean flow and turbulence quantities in most of the flow, and also is capable of predicting near-bed pressure accurately enough to compute form drag to within less than 10 percent. A video of the results of the DNS calculation can be displayed by clicking here [25mb]. The figures below can be enlarged simply be clicking on them.
Results
Click on any figure to enlarge
The results of this model are surprisingly independent of sub-grid scale closure, as the turbulence field appears to be dominated by relatively large scale structures associated with flow separation. This is not true very near the bed, and the DNS model shows significant deviations from the measured Reynolds stresses only in that area, and only relatively near the bedform crest, where the internal boundary layer is well developed. Although the DNS approach performs well, it is extremely computationally intensive, and is unwieldy for using in a morphodynamics code due to the computational time required for solution. Notably, the requirement of three-dimensional calculation even for two-dimensional flows is prohibitive.
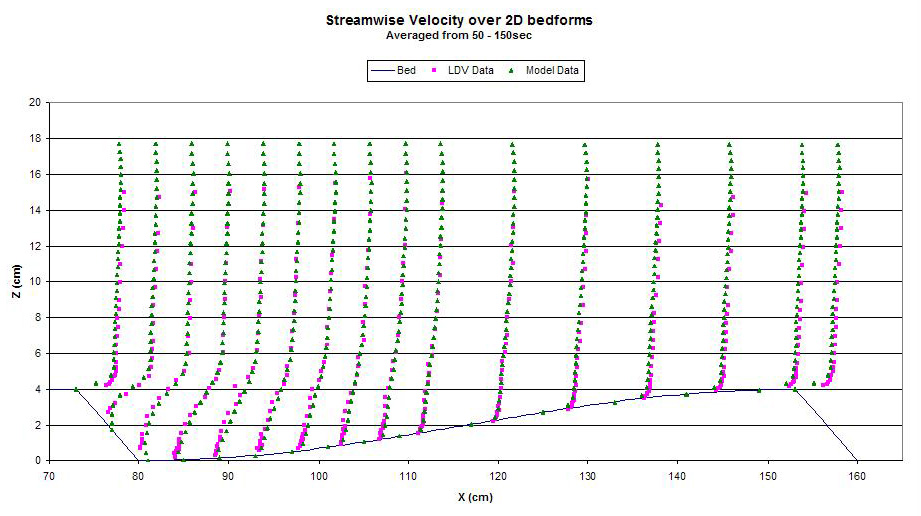
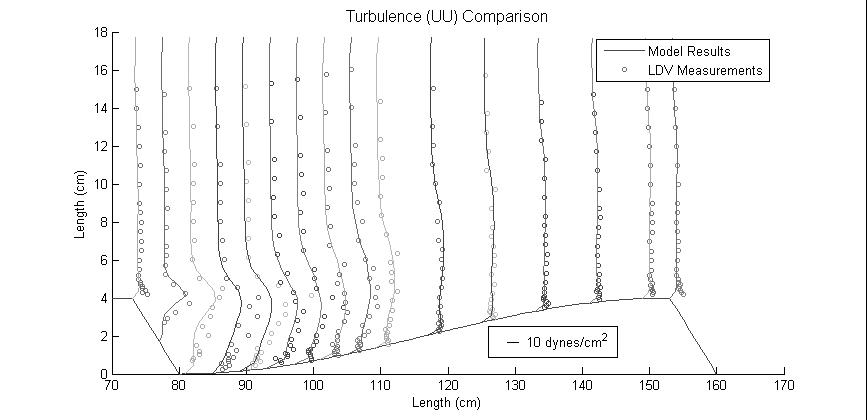
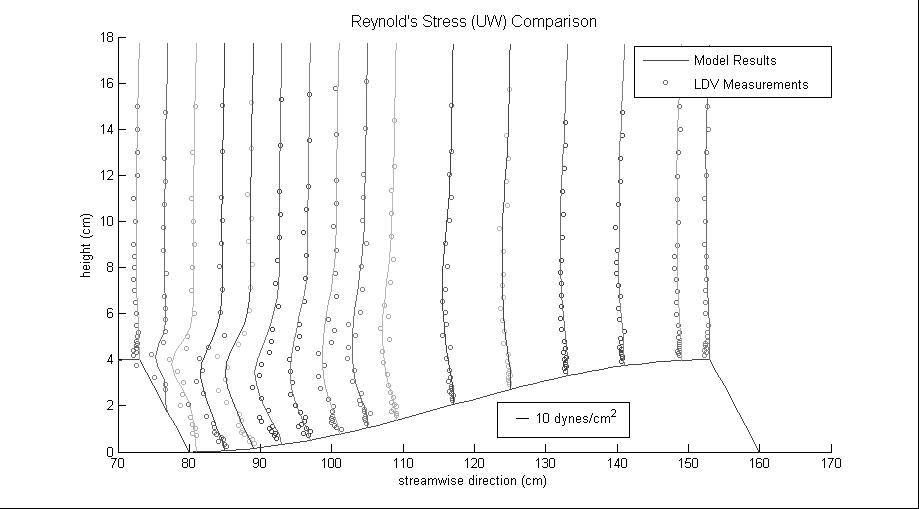
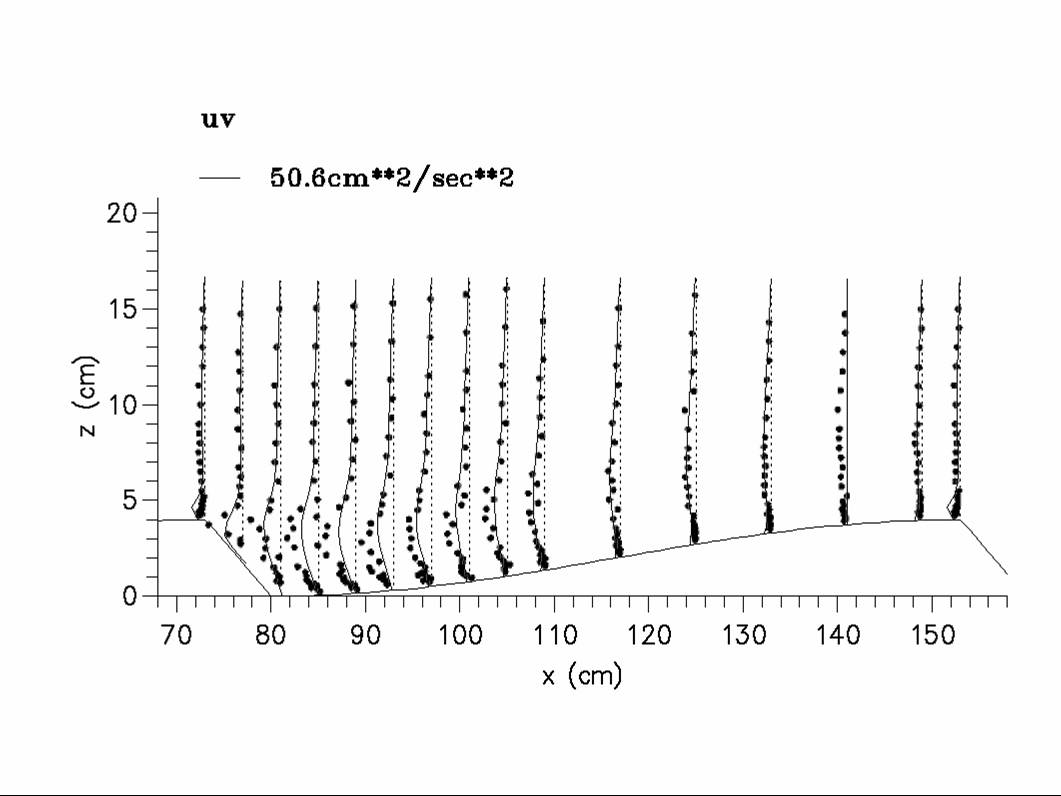
To circumvent these difficulties, we also developed an unsteady flow solution that employed turbulence closure. As found by other authors, our work suggests that a nonlinear k- closure is the simplest closure that works reasonably well for separated flows. Using a combination of the direct numerical simulation results and measured laboratory values to guide calibration, we were able to get numerical solutions close to the accuracy of the DNS solution by using a closure-type model. Two figures showing the comparison between measured values and values predicted by using this simpler model are shown below:
Although these comparisons show that the simpler approach is not as accurate as the DNS model, the agreement is only somewhat worse. Thus, the simpler model, which takes more than an order of magnitude less computational time, was subsequently coupled with a entrainment/distrainment model of sediment transport that explicitly treats the near-bed flow variability in computing transport (that is, it does not depend on time- or ensemble-averaged quantities). To test this component of the modeling approach, we used the model to predict flow and sediment motion downstream of a backward step and compared results to measurements made by using coupled laser-Doppler velocimetry and high-speed photography (Video [1.5mb]). We also compared these predictions to simpler sediment-transport models. Our approach agrees better with the data and also predicts important physical effects that are missed by using a simpler approach. Finally, we applied the combined flow and sediment motion model to examine the behavior of bedforms (link to new video I put on ftp site). Early results are encouraging, and use of this approach for practical problems involving bedform formation and response to time-varying flows appears promising.
Videos
Vorticity calculation from the DNS model.

Flow and Sediment Transport downstream of a backward step from the large-eddy simulation.