Sediment Transport Modeling
One of the principal goals of the research carried out at GSTL is to develop improved methods for computing sediment transport, especially in realistic, complex flows that have strong spatial or temporal accelerations. Most of what scientists currently know about sediment motion has been developed for very simple flows that are steady and uniform, unlike the flows that are found in nature. While empirical methods developed from simple flows are adequate for some more complicated natural flows, the largest barrier to making more accurate predictions of the morphologic evolution of rivers and other natural flows is the relatively poor capability of predicting sediment entrainment and local erosion and deposition.
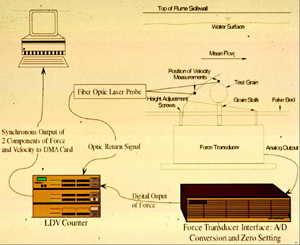
To address this problem, researchers at GSTL and their collaborators are working on developing better understanding of the mechanics of sediment movement by using experiments and computational models. Experiments typically involve making detailed measurements of sediment motion under carefully characterized flows, such as under waves or downstream of separation points, using particle-image velocimetry and high-speed videography and photography. We also developed a force transducer capable of measuring the forces on sediment grains at 200hz. Using this information, we are working on sediment entrainment and transport models that are developed based on the particle equations of motion (Newton’s Laws for the sediment particles). We are also working toward making detailed pressure measurements at high frequencies by using a new transducer and with a combination of pressure sensitive paints and high-speed videography. The videos and photos below show some example of this kind of work:
Force transducer measurements
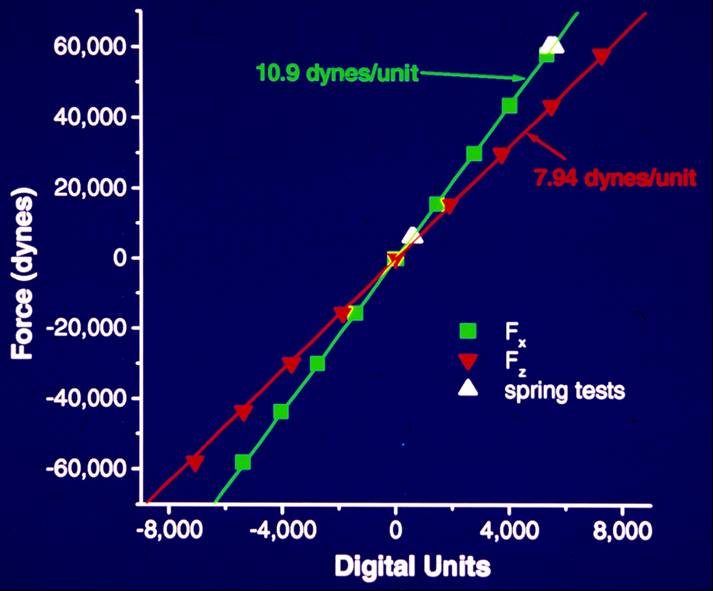
Using a force transducer developed jointly with Bill Bruner of Hylozoic Products, researcher from GSTL made direct measurements of forces on a particle in a variety of different flows. Using a laser-Doppler velocimeter, velocity measurements were made near the sediment particle while forces were measured; thus we could correlate flow events with force variations.
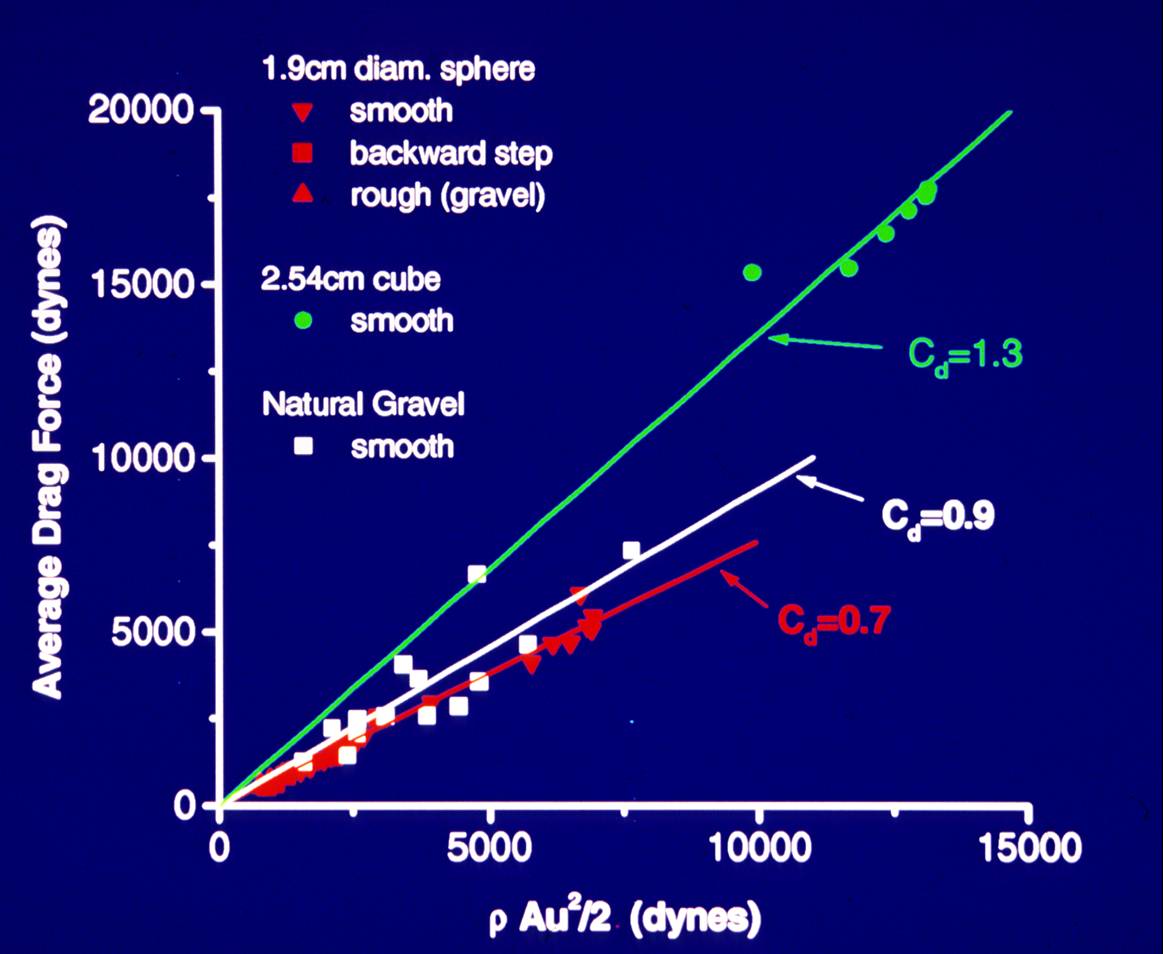
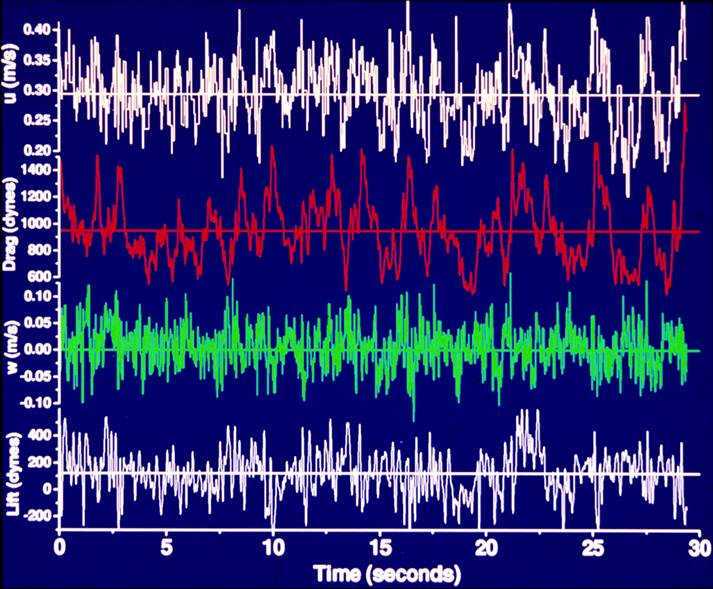
The data we obtained enabled us to check previous results for drag coefficients on sediment grains. Our experiments
showed that the effective drag coefficients were much larger than those found in simple settling experiments,
showing the importance of the near-bed turbulence field.
By comparing results for force distributions under different flow conditions as shown here, it was possible to characterize the string variability of drag and lift forces, which is extremely important for predicting sediment entrainment and transport. Almost all previous models base transport or entrainment on mean quantities, but rare excursions are of dominant importance. See our publications for more details on this work.
Computational Models of Bedload Motion
Using what we learned from the force transducer experiments, we developed a preliminary model for sediment motion based on first principles. This video of computational results developed by Mark Schmeeckle (as part of his work as a Ph.D student at University of Colorado; Mark is now a faculty member at Arizona State) for spheres shows the episodic nature of transport.

Sediment Transport Under Waves
We made measurements of bedload sediment flux under an oscillatory boundary layer at intermediate Reynolds numbers using the U-tube facility at the Technical University of Denmark with our collaborators Jorgen Fredsoe, Mutlu Sumer, and Karsten Lodahl. In this flow, it is possible to decouple the near-bed velocity and stress (or to change how they are coupled at different phases of a wave). By ensemble averaging near-bed flow measurements and using high-speed photography to digitize sediment motion, it was possible to examine the relationship between near-bed flow and motion for different kinds of turbulence structure.
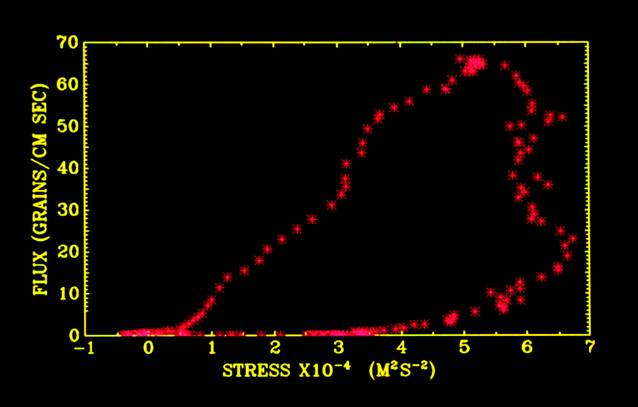
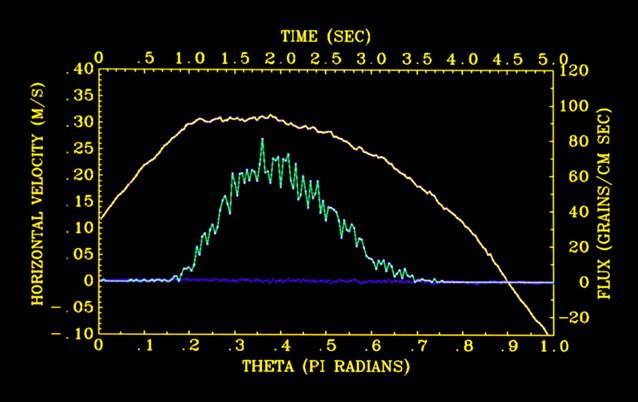
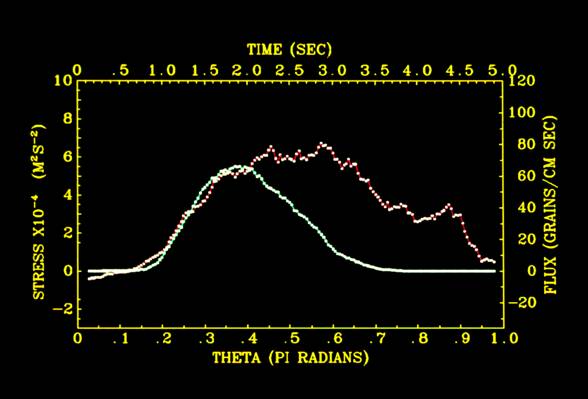
This graph shows the relation between stress and sediment flux. Note that the relation shows significant hysteresis, with
sediment flux changing greatly for different values of the bed stress. This is because the velocity field
(which drives lift and drag on the particles) is not tied directly to the stress because of the acceleration of the flow.
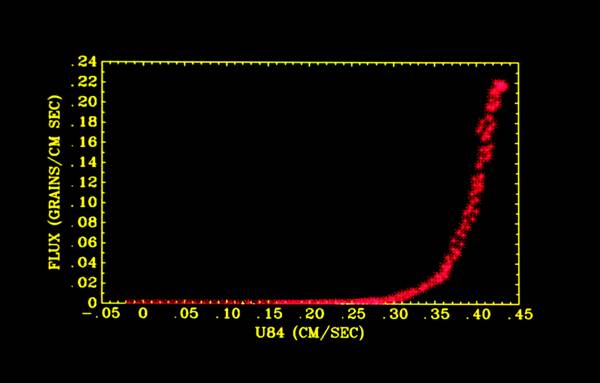
If we plot sediment transport against some high percentile of the velocity distribution at each phase of the wave, we
obtain a very tight relationship that cannot be obtained by predicting transport from the stress. This is a very
simple example of the role of acceleration in complex flows on sediment entrainment and transport.